
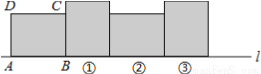
如图,在矩形ABCD中,已知AB=2,BC=1.5,矩形在直线上绕其右下角的顶点B向右第一次旋转90°至图①位置,再绕右下角的顶点继续向右第二次旋转90°至图②位置,…,以此类推,这样连续旋转2017次后,顶点A在整个旋转过程中所经过的路程之和是_______.
科目:初中数学 来源:2017-2018学年七年级数学下册(遵义):期中检测题 题型:单选题
在平面直角坐标系中,若点P(a,b)在第二象限,则点Q(2﹣a,﹣1﹣b)在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
D 【解析】∵在平面直角坐标系中,点P(a,b)在第二象限, ∴ , ∴ , ∴点Q(2-a,-1-b)在第四象限. 故选D.查看答案和解析>>
科目:初中数学 来源:山东省潍坊市高密市2017-2018学年七年级(上)期中数学试卷 题型:填空题
若a,b互为相反数,m,n互为倒数,则(a+b)2018﹣(﹣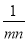 )2017=_____.
)2017=_____.
查看答案和解析>>
科目:初中数学 来源:山东省潍坊市高密市2017-2018学年七年级(上)期中数学试卷 题型:单选题
下列调查中,最适合用普查方式的是( )
A. 调查一批电视机的使用寿命情况
B. 调查某中学九年级一班学生的视力情况
C. 调查重庆市初中学生每天锻炼所用的时间情况
D. 调查重庆市初中学生利用网络媒体自主学习的情况
B 【解析】试题分析:选择调查方式的原则是:方便、易操作、工作量不大、不带破坏性。A选项具有破坏性;C、D范围大、不易操作、工作量极其庞大、费时费财力。故选:B.查看答案和解析>>
科目:初中数学 来源:浙江省余姚市2018届九年级上学期期中考试数学试卷 题型:解答题
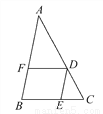
如图,DE∥AB,FD∥BC, 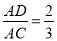 ,AB=9cm,BC=6cm,则四边形BEDF的周长是多少?
,AB=9cm,BC=6cm,则四边形BEDF的周长是多少?
查看答案和解析>>
科目:初中数学 来源:浙江省余姚市2018届九年级上学期期中考试数学试卷 题型:单选题
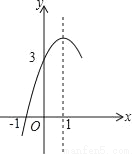
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;
②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;
③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )
A. 4个 B. 3个 C. 2个 D. 1个
B 【解析】解:∵抛物线与x轴有2个交点,∴b2﹣4ac>0,所以①正确; ∵抛物线的对称轴为直线x=1,而点(﹣1,0)关于直线x=1的对称点的坐标为(3,0),∴方程ax2+bx+c=0的两个根是x1=﹣1,x2=3,所以②正确; ∵x=﹣=1,即b=﹣2a,而x=﹣1时,y=0,即a﹣b+c=0,∴a+2a+c=0,所以③错误; ∵抛物线与x轴的两点坐标为(﹣1,0)...查看答案和解析>>
科目:初中数学 来源:云南省2017-2018学年七年级上学期期中考试数学试卷 题型:解答题
先化简,再求值:
(5x2-3y2)-[(5x2-2xy-y2)-(x2-2xy+3y2)],其中x=2,y= -1.
,5. 【解析】试题分析:原式去括号合并得到最简结果,把x与y的值代入计算即可求出值. 试题解析:【解析】 原式=5x2-3y2-5x2+2xy+y2+x2-2xy+3y2=x2+y2, 当x=2,y=-1时,原式=4+1=5.查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:解答题
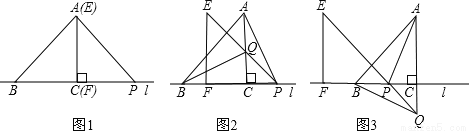
如图,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线 l上,边EF与边AC重合,且EF=FP.
(1)在图1中,请你通过观察、测量,猜想并写出AB与AP所满足的数量关系和位置关系;
(2)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连结AP,
BQ.猜想并写出BQ 与AP 所满足的数量关系和位置关系,请证明你的猜想;
(3)AP,BQ .你认为(2)中所猜想的BQ 与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期八年级数学期中试卷 题型:解答题
解分式方程:(1)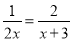 (2)
(2) 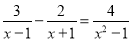
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com