
在﹣2、﹣1、0、1、2、3这六个数中,任取两个数,恰好互为相反数的概率为( )
A. 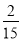 B.
B. 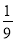 C.
C. 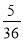 D.
D. 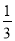
科目:初中数学 来源:江苏省苏州市2017年中考数学二模试卷 题型:单选题
若a<2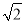 <b,其中a、b为两个连续的整数,则ab的值为 ( )
<b,其中a、b为两个连续的整数,则ab的值为 ( )
A. 2 B. 5 C. 6 D. 12
C 【解析】, , , 为连续整数, ∴, , ∴. 故选:C.查看答案和解析>>
科目:初中数学 来源:山东省德州市2018届九年级上期中数学试卷 题型:填空题
若A(﹣4,y1),B(﹣3,y2),C(1,y3)为二次函数y=x2+4x﹣m的图象上的三点,则y1,y2,y3的大小关系是_____.
y3>y1>y2 【解析】分别计算出自变量为﹣4,﹣3和1所对应的函数值,然后比较函数值的大小即可. 【解析】 当x=﹣4时,y1=x2+4x﹣m=16﹣16﹣m=﹣m; 当x=﹣3时,y2=x2+4x﹣m=9﹣12﹣m=﹣3﹣m; 当x=1时,y3=x2+4x﹣m=1+4﹣m=5﹣m; 所以y3>y1>y2. 故答案为y3>y1>y2.查看答案和解析>>
科目:初中数学 来源:2017年海南省海口市中考数学模拟试卷 题型:解答题
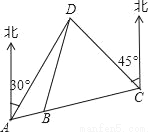
某市开展一项自行车旅游活动,线路需经A、B、C、D四地,如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27, 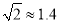 ,
, 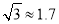 .)
.)
查看答案和解析>>
科目:初中数学 来源:2017年海南省海口市中考数学模拟试卷 题型:填空题
在一幅长50cm,宽30cm的风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个规划土地的面积是1800cm2,设金色纸边的宽为xcm,那么x满足的方程为_____.
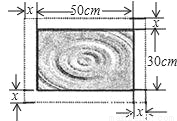
查看答案和解析>>
科目:初中数学 来源:2017年海南省海口市中考数学模拟试卷 题型:单选题
2017年我国大学生毕业人数将达到7490000人,这个数据用科学计数法表示为( )
A. 7.49×107 B. 7.49×106 C. 74.9×106 D. 0.749×107
B 【解析】试题分析:将7 490 000用科学记数法表示为:7.49×106. 故选B.查看答案和解析>>
科目:初中数学 来源:江苏省丹阳市2017-2018学年七年级12月月考数学试卷 题型:解答题
观察下列等式:
第一个等式:a1=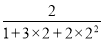 =
=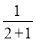 -
-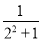
第二个等式:a2= =
=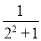 -
-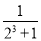
第三个等式:a3= =
=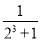 -
-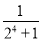
第四个等式:a4= =
=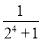 -
-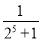
按上述规律,回答下列问题:
(1)请写出第六个等式:a6=_____=_____;
(2)用含n的代数式表示第n个等式:an=_____=_____;
(3)a1+a2+a3+a4+a5+a6=_____(得出最简结果);
(4)计算:a1+a2+…+an.
(1), -;(2), -;(3);(4). 【解析】(1)根据已知4个等式可得; (2)根据已知等式得出答案; (3)利用所得等式的规律列出算式,然后两两相消,计算化简后的算式即可得; (4)根据已知等式规律,列项相消求解可得. 【解析】 (1)由题意知,a6==-, (2)an==-, (3)原式=﹣+﹣+﹣+﹣+﹣+﹣ =﹣ =, ...查看答案和解析>>
科目:初中数学 来源:江苏省丹阳市2017-2018学年七年级12月月考数学试卷 题型:填空题
方程(2a-1)x2+3x+1=4是一元一次方程,则a= ______ .
【解析】由题意得2a-1=0,解得a= .查看答案和解析>>
科目:初中数学 来源:吉林省松原市2018届九年级上期末模拟数学试卷 题型:填空题
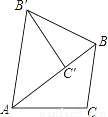
如图,把△ABC绕点A逆时针旋转42°,得到△AB′C′,点C′恰好落在边AB上,连接BB′,则∠B′BC′的大小为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com