
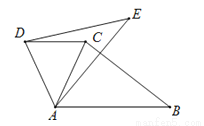
如图,在同一平面内,将△ABC绕点A逆时针旋转40°到△AED的位置,恰好使得DC∥AB,则∠CAB的大小为______________.
科目:初中数学 来源:广西合浦县2017年秋季学期教学质量监测八年级数学试卷 题型:解答题
计算:
(1)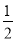 m2-n(mn2)2;
m2-n(mn2)2;
(2)(x2-2x)(2x+3)÷(2x);
(3)(2x+y)(2x-y)+(x+y)2-2(2x2+xy);
(4)(ab-b2)÷ .
.
查看答案和解析>>
科目:初中数学 来源:广西合浦县2017年秋季学期教学质量监测九年级数学试卷 题型:解答题
知识是用来为人类服务的,我们应该把它们用于有意义的方面.下面就两个情景请你作出评判.
情景一:从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?试用所学数学知识来说明这个问题.
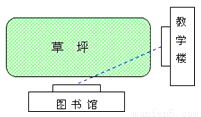
情景二:A、B 是河流l两旁 的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由:
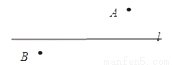
你赞同以上哪种做法?你认为应用数学知识为人类服务时应注意什么?
情景一:两点之间线段最短;情景二:两点指点线段最短 【解析】试题分析:根据两点之间的所有连线中,线段最短,作答即可. 试题解析:情景一:因为教学楼和图书馆处于同一条直线上,两点之间的所有连线中,线段最短,所以这样走比较近; 情景二:抽水站点P的位置如右图所示: 理由:两点之间的所有连线中,线段最短; 赞同情景二中运用知识的做法,应用数学知识为人类服务时应注意:不能以破...查看答案和解析>>
科目:初中数学 来源:广西合浦县2017年秋季学期教学质量监测九年级数学试卷 题型:单选题
某几何体的三视图如图,则该几何体是( )

A. 圆柱 B. 圆锥 C. 球 D. 长方体
B 【解析】试题解析:从主视图和左视图可以看出这个几何体是椎体,从俯视图可以看出这个几何体不是棱锥,是圆锥, 故选A.查看答案和解析>>
科目:初中数学 来源:山东省滨州市惠民县2018届九年级上学期期末数学试卷 题型:解答题
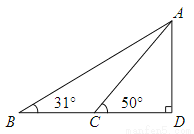
据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s在一条笔直公路BD的上方A处有一探测仪,如平面几何图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°(tan31°≈0.6,tan50°≈1.2,结果精确到1m).
(1)求B,C的距离.
(2)通过计算,判断此轿车是否超速.
查看答案和解析>>
科目:初中数学 来源:山东省滨州市惠民县2018届九年级上学期期末数学试卷 题型:单选题
若反比例函数y=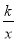 与一次函数y=x-3的图象没有交点,则k的值可以是
与一次函数y=x-3的图象没有交点,则k的值可以是
A. 1 B. -1 C. -2 D. -3
D 【解析】∵反比例函数y=与一次函数y=x-3的图象没有交点, ∴关于x的方程无实数解, ∴关于x的一元二次方程: 无实数根, ∴,解得: , ∴上述四个选项中,只有D选项中的数符合要求. 故选D.查看答案和解析>>
科目:初中数学 来源:山东省滨州市惠民县2018届九年级上学期期末数学试卷 题型:单选题
在6张完全相同的卡片上分别画上线段、等边三角形、平行四边形、直角梯形、正方形、圆,在看不见图形的情况下随机摸出1张,这张卡片上的图形既是中心对称图形又是轴对称图形的概率是
A. 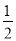 B.
B. 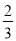 C.
C. 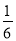 D.
D. 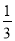
查看答案和解析>>
科目:初中数学 来源:湖南省雨花新华都学校2017-2018学年七年级(上)第一次月考数学试卷 题型:单选题
(2015永州)定义[x]为不超过x的最大整数,如[3.6]=3,[0.6]=0,[﹣3.6]=﹣4.对于任意实数x,下列式子中错误的是( )
A. [x]=x(x为整数) B. 0≤x﹣[x]<1 C. [x+y]≤[x]+[y] D. [n+x]=n+[x](n为整数)
C 【解析】试题分析:解决本题的关键就是理解新定义的含义.当x=5.5,y=4.6时,[x+y]=[10.1]=10,[x]+[y]=5+4=9,则[x+y]>[x]+[y],则C选项错误.查看答案和解析>>
科目:初中数学 来源:安徽省蚌埠市2017届九年级下学期中考一模数学试卷 题型:解答题
已知:如图,斜坡AP的坡度为1:2.4,坡长AP为26米,在坡顶A处的同一水平面上有一座古塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶B的仰角为76°.求:
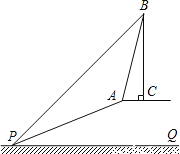
(1)坡顶A到地面PQ的距离;
(2)古塔BC的高度(结果精确到1米).(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
(1)10m,(2)古塔BC的高度约为19米. 【解析】 试题分析:(1)过点A作AH⊥PQ,垂足为点H,利用斜坡AP的坡度为1:2.4,得出AH,PH,AP的关系求出即可; (2)利用矩形性质求出设BC=x,则x+10=24+DH,再利用tan76°=,求出即可. 试题解析:(1)过点A作AH⊥PQ,垂足为点H. ∵斜坡AP的坡度为1:2.4, ∴, 设...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com