
计算:20172-20162=____________.
4033 【解析】20172-20162=(2017+2016)×(2017-2016)=4033. 故答案为:4033. 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:四川省江县初中2016年秋季八年级期末考试试卷 题型:填空题
将数0.000000015用科学记数法表示为_____.
1.5×10﹣8 【解析】0.000000015用科学记数法表示为:0.000000015=1.5×10-8.查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:解答题
已知如图,将一大、一小两个等腰直角三角尺ABC与DBE拼接(A、B、D三点共线,AB=CB,EB=DB,∠ABC =∠EBD=90°),连接AE、CD.问:AE与CD的位置关系和数量关系,并证明你的结论.
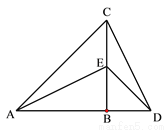
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:填空题
如右图,△ABC是等腰直角三角形,∠C=90°,BD平分∠CBA交AC于点D,DE⊥AB于E.若△ADE的周长为8cm,则AB =_________ cm.
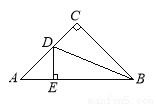
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:单选题
已知三角形的两边长分别为3和7,则第三边的中线长x的取值范围是( )
A. 2<x<5 B. 4<x<10 C. 3<x<7 D. 无法确定
A 【解析】如图所示,AB=3,AC=7,延长AD至E,使AD=DE,连接BE、EC, 设AD=x, 在△BDE与△CDA中,, ∴△BDE≌△CDA(SAS), ∴BE=AC=7,AE=2x, 在△ABE中,BE?AB查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:单选题
下列各式中,正确的是( )
A. 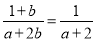 B.
B. 
C. 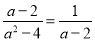 D.
D. 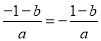
查看答案和解析>>
科目:初中数学 来源:北京市平谷区2018届初三第一学期期末数学试卷 题型:填空题
“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣.”这是我国古代著名数学家刘徽在《九章算术注》中提到的“如何求圆的周长和面积”的方法,即“割圆术”.“割圆术”的主要意思是用圆内接正多边形去逐步逼近圆.刘徽从圆内接正六边形出发,将边数逐次加倍,并逐次得到正多边形的周长和面积.如图,AB是圆内接正六边形的一条边,半径OB=1,OC⊥AB于点D,则圆内接正十二边形的边BC的长是_________________(结果不取近似值).
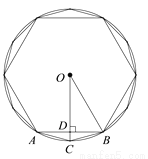
查看答案和解析>>
科目:初中数学 来源:上海浦东新区2017-2018学年九年级上学期期末数学试卷(初三一模) 题型:解答题
如图,已知△ABC中,点D、E分别在边AB和AC上,DE∥BC,且DE经过△ABC的重心,设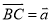 .
.
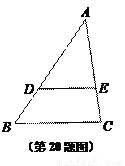
(1)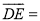 (用向量
(用向量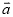 表示);
表示);
(2)设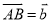 ,在图中求作
,在图中求作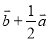 .
.
(不要求写作法,但要指出所作图中表示结论的向量.)
(1);(2)详见解析. 【解析】试题分析:(1)由DE∥BC,DE经过△ABC的重心,可得AD:AB=DE:BC=2:3,即可求得; (2)取点BC的中点M,连接AM,则即为所求. 试题解析:(1)∵DE∥BC,DE经过△ABC的重心, ∴AD:AB=DE:BC=2:3,, ∵, ∴ ; (2)如图,取点AB的中点M,连接AM,则即为所求.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com