
某小区有一块边长为a的正方形场地,规划修建两条宽为b的绿化带.方案一如图甲所示,绿化带面积为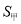 ;方案二如图乙所示,绿化带面积为
;方案二如图乙所示,绿化带面积为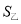 .设
.设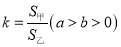 ,下列选项中正确的是( )
,下列选项中正确的是( )
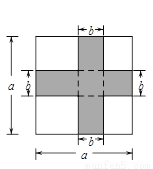
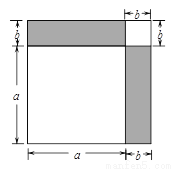
甲 乙
A. 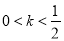 B.
B. 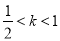 C.
C. 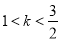 D.
D. 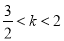
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2017-2018学年八年级数学下册(华师大版):期末检测1 题型:单选题
如图,在平行四边形ABCD中,AE平分∠BAD,CE=4 cm,AB=5 cm,则平行四边形ABCD的周长是( )
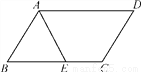
A. 18 cm B. 26 cm C. 28 cm D. 29 cm
C 【解析】试题解析:∵四边形ABCD是平行四边形, ∴AD∥BC, ∴∠DAE=∠AEB. ∵AE平分∠BAD, ∴∠BAE=∠DAE, ∴∠BAE=∠AEB, ∴BE=AB=5cm, ∴BC=BE+EC=5+4=9cm. ∴平行四边形ABCD的周长为:2×(9+5)=28(cm). 故选C.查看答案和解析>>
科目:初中数学 来源:湖北省孝感市八校联谊2017-2018学年九年级上册数学12月联考试卷 题型:填空题
若 x1,x2是方程x2-2mx+m2-m-1 的两个实数根,且x1+x2=1-x1x2 ,则m 的值为________.
1 【解析】若x1,x2是方程x2-2mx+m2-m-1的两个实数根; ∴x1+x2=2m;x1·x2= m2?m?1, ∵x1+x2=1-x1x2, ∴2m=1-(m2?m?1), 解得:m1=-2,m2=1. 又∵一元二次方程有实数根时,△ , ∴, 解得m≥-1, ∴m=1. 故答案为:1.查看答案和解析>>
科目:初中数学 来源:北京海淀区2017-2018学年初二第一学期数学期末试卷 题型:解答题
先化简,再求值: 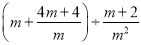 ,其中
,其中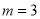 .
.
查看答案和解析>>
科目:初中数学 来源:北京海淀区2017-2018学年初二第一学期数学期末试卷 题型:填空题
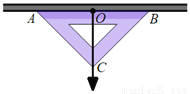
某地地震过后,小娜同学用下面的方法检测教室的房梁是否处于水平:在等腰直角三角尺斜边中点O处拴一条线绳,线绳的另一端挂一个铅锤,把这块三角尺的斜边贴在房梁上,结果线绳经过三角尺的直角顶点,由此得出房梁是水平的(即挂铅锤的线绳与房梁垂直).用到的数学原理是_______________.
查看答案和解析>>
科目:初中数学 来源:北京海淀区2017-2018学年初二第一学期数学期末试卷 题型:单选题
如图,点D,E在△ABC的边BC上,△ABD≌△ACE,其中B,C为对应顶点,D,E为对应顶点,下列结论不一定成立的是( )
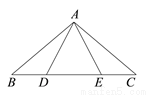
A. AC=CD B. BE=CD C. ∠ADE=∠AED D. ∠BAE=∠CAD
A 【解析】∵△ABD≌△ACE,∴∠ADB=∠AEC,∠BAD=∠CAE,BD=CD, ∴180°-∠ADB=180°-∠AEC,∠BAD+∠DAE=∠CAE+∠DAE,BD+DE=CE+DE, 即∠ADE=∠AED,∠BAE=∠CAD,BE=CD, 故B、C、D选项成立,故不符合题意; 无法证明AC=CD,故A符合题意, 故选A.查看答案和解析>>
科目:初中数学 来源:北京市海淀区2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
阅读材料
小明遇到这样一个问题:求计算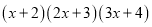 所得多项式的一次项系数.
所得多项式的一次项系数.
小明想通过计算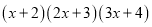 所得的多项式解决上面的问题,但感觉有些繁琐,他想探寻一下,是否有相对简洁的方法.
所得的多项式解决上面的问题,但感觉有些繁琐,他想探寻一下,是否有相对简洁的方法.
他决定从简单情况开始,先找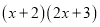 所得多项式中的一次项系数.通过观察发现:
所得多项式中的一次项系数.通过观察发现:
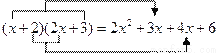
也就是说,只需用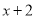 中的一次项系数1乘以
中的一次项系数1乘以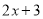 中的常数项3,再用
中的常数项3,再用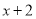 中的常数项2乘以
中的常数项2乘以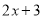 中的一次项系数2,两个积相加
中的一次项系数2,两个积相加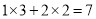 ,即可得到一次项系数.
,即可得到一次项系数.
延续上面的方法,求计算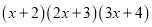 所得多项式的一次项系数.可以先用
所得多项式的一次项系数.可以先用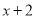 的一次项系数1,
的一次项系数1, 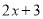 的常数项3,
的常数项3, 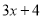 的常数项4,相乘得到12;再用
的常数项4,相乘得到12;再用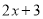 的一次项系数2,
的一次项系数2, 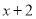 的常数项2,
的常数项2, 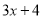 的常数项4,相乘得到16;然后用
的常数项4,相乘得到16;然后用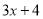 的一次项系数3,
的一次项系数3, 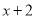 的常数项2,
的常数项2, 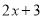 的常数项3,相乘得到18.最后将12,16,18相加,得到的一次项系数为46.
的常数项3,相乘得到18.最后将12,16,18相加,得到的一次项系数为46.
参考小明思考问题的方法,解决下列问题:
(1)计算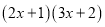 所得多项式的一次项系数为 .
所得多项式的一次项系数为 .
(2)计算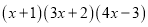 所得多项式的一次项系数为 .
所得多项式的一次项系数为 .
(3)若计算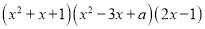 所得多项式的一次项系数为0,则
所得多项式的一次项系数为0,则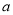 =_________.
=_________.
(4)若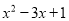 是
是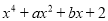 的一个因式,则
的一个因式,则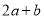 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源:北京市海淀区2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
在平面直角坐标系xOy中,以原点O为圆心,任意长为半径作弧,分别交x轴的负半轴和y轴的正半轴于A点,B点.分别以点A,点B为圆心,AB的长为半径作弧,两弧交于P点.若点P的坐标为(a,b),则( )
A. 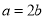 B.
B. 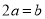 C.
C. 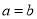 D.
D. 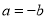
查看答案和解析>>
科目:初中数学 来源:福建省2017-2018学年九年级数学上学期期末检测试卷 题型:解答题
已知抛物线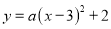 经过点(1,-2).
经过点(1,-2).
(1)求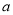 的值;
的值;
(2)若点A(m,y1)、B(n,y2)(m<n<3)都在该抛物线上,试比较y1与y2的大小.
(1)a=-1;(2)y1<y2. 【解析】试题分析:(1)、将点(1,-2),利用待定系数法求出函数解析式;(2)、首先得出二次函数的对称轴,然后根据函数的性质求出大小. 试题解析:(1)、∵抛物线经过点(1,-2), ∴,解得a=-1; (2)、∵函数的对称轴为x=3, ∴ A(m,y1)、B(n,y2)(m<n<3)在对称轴左侧, 又∵抛物线开口向下,∴ 对称轴...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com