练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    求不等式组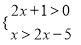的正整数解．

    1，2，3，4． 【解析】试题分析：先求出不等式组的解集，再从不等式组的解集中找出适合条件的正整数即可． 试题解析：解不等式2x+1＞0，得：x＞-， 解不等式x＞2x-5，得：x＜5， ∴不等式组的解集为-＜x＜5， ∵x是正整数， ∴x=1、2、3、4．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：江苏省盐城市2017-2018学年八年级12月月考数学试卷 题型：填空题

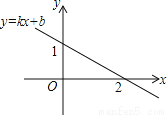
    已知一次函数y=kx+b的图象如图，则y＞1时x的取值范围是_________．

    x＜0 【解析】由图像可知，当x＜0时，y＞1， ∴y＞1时x的取值范围是：x＜0.

    查看答案和解析>>

    科目：初中数学 来源：甘肃省定西市安定区2016-2017学年八年级上学期期末考试数学试卷 题型：单选题

    下列“无人看守铁路道口，窄桥，限速40，向右急转弯”四个交通标志图中，为轴对称图形的是（ ）

    A. B. C. D.

    B 【解析】试题解析：A、不是轴对称图形，故本选项错误； B、是轴对称图形，故本选项正确； C、不是轴对称图形，故本选项错误； D、不是轴对称图形，故本选项错误． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：山东省滨州市部2017-2018学年八年级（上）第一次月考数学试卷 题型：单选题

    对于任意三角形的高，下列说法不正确的是（ ）

    A. 锐角三角形有三条高 B. 直角三角形只有一条高

    C. 任意三角形都有三条高 D. 钝角三角形有两条高在三角形的外部

    B 【解析】试题分析：根据三角形的高的概念，通过具体作高，发现：任意一个三角形都有三条高，其中锐角三角形的三条高都在三角形的内部；直角三角形有两条高即三角形的两条直角边，一条在内部；钝角三角形有两条高在三角形的外部，一条在内部，据此可知： A、锐角三角形有三条高，说法正确，故本选项不符合题意； B、直角三角形有三条高，说法错误，故本选项符合题意； C、任意三角形都有三条高，...

    查看答案和解析>>

    科目：初中数学 来源：广西崇左市天等县2017年中考数学一模试卷 题型：解答题

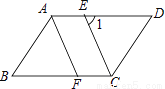
    已知平行四边形ABCD中，CE平分∠BCD且交AD于点E，AF∥CE，且交BC于点F．

    （1）求证：△ABF≌△CDE；

    （2）如图，若∠1=65°，求∠B的大小．

    （1）证明见解析；（2）50°． 【解析】试题分析：（1）由平行四边形的性质得出AB=CD，AD∥BC，∠B=∠D，得出∠1=∠DCE，证出∠AFB=∠1，由AAS证明△ABF≌△CDE即可；（2）由（1）得∠1=∠DCE=65°，由平行四边形的性质和三角形内角和定理即可得出结果． 试题解析：（1）∵四边形ABCD是平行四边形， ∴AB=CD，AD∥BC，∠B=∠D， ∴∠1=∠DCE...

    查看答案和解析>>

    科目：初中数学 来源：广西崇左市天等县2017年中考数学一模试卷 题型：填空题

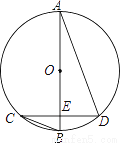
    如图，⊙O的直径AB过弦CD的中点E，若∠C=25°，则∠D=________．

    65° 【解析】试题分析：先根据圆周角定理求出∠A的度数，再由垂径定理求出∠AED的度数，进而可得出结论． ∵∠C=25°， ∴∠A=∠C=25°． ∵⊙O的直径AB过弦CD的中点E， ∴AB⊥CD， ∴∠AED=90°， ∴∠D=90°﹣25°=65°

    查看答案和解析>>

    科目：初中数学 来源：广西崇左市天等县2017年中考数学一模试卷 题型：单选题

    如图，已知在⊙O中，AB是弦，半径OC⊥AB，垂足为点D，要使四边形OACB为菱形，还需要添加一个条件，这个条件可以是（   ）

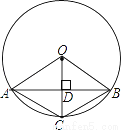
    A. AD=BD B. OD=CD C. ∠CAD=∠CBD D. ∠OCA=∠OCB

    B 【解析】DO=CD.理由如下： ∵在O中，AB是弦，半径OC⊥AB， ∴AD=DB， ∵DO=CD， ∴AD=BD，DO=CD，AB⊥CO， ∴四边形OACB为菱形.故选B.

    查看答案和解析>>

    科目：初中数学 来源：山东省2018届九年级上学期第三次月考数学试卷 题型：填空题

    已知方程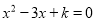有两个相等的实数根，则=_______．

    ． 【解析】试题分析：由题意得，根的判别式△=b2-4ac=（-3）2-4k=0，解得k=．

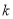    查看答案和解析>>

    科目：初中数学 来源：黄金30题系列 九年级数学 大题好拿分 题型：解答题

    大润发超市以每件30元的价格购进一种商品，试销中发现每天的销售量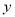（件）与每件的销售价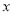（元）之间满足一次函数.

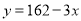    （1）、写出超市每天的销售利润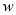（元）与每件的销售价x（元）之间的函数关系式；

    （2）、如果超市每天想要获得销售利润420元，则每件商品的销售价应定为多少元？

    （3）、如果超市要想获得最大利润，每件商品的销售价定为多少元最合适？最大销售利润为多少元？

    （1）、w=－3+252x－4860；（2）、40或44；（3）、42元，432元. 【解析】 试题分析：（1）、根据销售利润=单件利润×数量求出；（2）、根据w=420列出一元二次方程，求出x的值；（3）、将二次函数配方成顶点式，然后进行说明. 试题解析：（1） ∴ （2）由题意知： ∴ ∴ ∴当销售价定为40或44元时，可获得420元的利润. （...

    查看答案和解析>>

    同步练习册答案