
先化简,再求值: 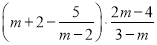 ,其中
,其中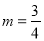 .
.
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源:北京市分校2017-2018学年度第一学期期中初二数学试卷 题型:填空题
轮船在静水中的速度是a千米/时,水流速度是b千米/时,则轮船逆流航行10千米所用时间为______小时.
. 【解析】∵轮船在静水中的速度是a千米/时,水流速度是b千米/时, ∴轮船的逆流速度为千米/时, ∴轮船逆流航行10千米所用时间为: 小时. 故答案为: .查看答案和解析>>
科目:初中数学 来源:上海市黄浦区2018届九年级上学期期末调研测试数学试卷(WORD版) 题型:解答题
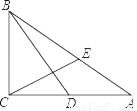
如图,在△ABC中,∠ACB=90°,AC=4,BC=3,D是边AC的中点,CE⊥BD交AB于点E.
(1)求tan∠ACE的值;
(2)求AE:EB.
查看答案和解析>>
科目:初中数学 来源:上海市黄浦区2018届九年级上学期期末调研测试数学试卷(WORD版) 题型:单选题
如图,线段AB与CD交于点O,下列条件中能判定AC∥BD的是( )
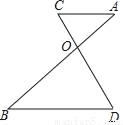
A. OC=1,OD=2,OA=3,OB=4 B. OA=1,AC=2,AB=3,BD=4
C. OC=1,OA=2,CD=3,OB=4 D. OC=1,OA=2,AB=3,CD=4.
C 【解析】根据平行线分线段成比例,因为,所以AC∥BD,故选C.查看答案和解析>>
科目:初中数学 来源:北京市西城外国语学校2017-2018学年度第一学期八年级数学期中试卷 题型:解答题
如图,在△ABC中,AD⊥BC于D, CE平分∠ACB分别交AB、AD于E、F两点,且BD=FD,AB=CF.求证:(1)CE AB;(2)AE=BE.
AB;(2)AE=BE.

查看答案和解析>>
科目:初中数学 来源:北京市西城外国语学校2017-2018学年度第一学期八年级数学期中试卷 题型:填空题
如图,已知∠1=∠2,AC=AD,添加一个条件使△ABC≌△AED,你添加的条件是__________(填一种即可),根据________________.

查看答案和解析>>
科目:初中数学 来源:北京市西城外国语学校2017-2018学年度第一学期八年级数学期中试卷 题型:填空题
若分式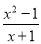 的值为0,则
的值为0,则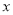 的值等于 .
的值等于 .
查看答案和解析>>
科目:初中数学 来源:黑龙江省大庆市2016---2017学年度上期初三数学期末试卷 题型:解答题
解方程: 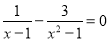 .
.
查看答案和解析>>
科目:初中数学 来源:浙江省余姚市2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
下列句子是命题的是( )
A. 画∠AOB=45° B. 小于直角的角是锐角吗?
C. 连结CD D. 三角形内角和等于180°
D 【解析】对于选项A、C,由于不能判断其正误,所以不是命题; 对于选项B,由于不是陈述句,所以不是命题; 对于选项D,根据命题的定义可得D中的句子是命题. 故选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com