练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

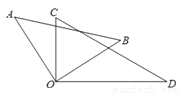
    如图，将一副三角板的直角顶点重合，摆放在桌面上，若∠BOC=63°，则∠AOD= __．

    117° 【解析】∵将一副三角板的直角顶点重合， ∴∠AOB=∠COD=90°， ∵∠BOC=63°， ∴∠AOC=27°， ∴∠AOD=∠COD+∠AOC=117°．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：广东省初中部2017-2018学年第一学期期末模拟测试七年级数学试卷 题型：单选题

    如图，直线a、b都与直线c相交，给出下列条件：（1）∠1=∠2；（2）∠3=∠6；（3）∠4+∠7=180°；（4）∠5+∠8=180°，其中能判断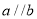的是（ ）

    A. （1）、（3） B. （2）、（4）

    C. （1）、（3）、（4） D. （1）、（2）、（3）、（4）

    D 【解析】（1）∵∠1=∠2，∴a∥b； （2）∵∠3=∠6，∴a∥b； （3）∵∠4+∠7=180°，∠4+∠2=180°， ∴∠7=∠2， ∴a∥b； （4）∵∠5+∠8=180°，∠5+∠7=180°， ∴∠7=∠8， ∴a∥b. 综上所述，4个条件都能判定a∥b. 故选D.

    查看答案和解析>>

    科目：初中数学 来源：云南省2016-2017学年七年级上学期期末考试数学试卷 题型：解答题

    解方程： .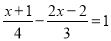

    x=﹣． 【解析】试题分析：先去分母，再去括号，移项合并同类项，系数化1. 试题解析： 去分母得：3（x+1）﹣4（2x﹣2）=12， 去括号得： 3x+3﹣8x+8=12， 移项、合并同类项得： ﹣5x=1， 系数化为1得： x=﹣ ．

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市2016-2017学年七年级上学期期末考试数学试卷 题型：解答题

    如图1，点O为直线AB上一点，过点O作射线OC，使∠BOC=120°．将一直角三角板的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方．

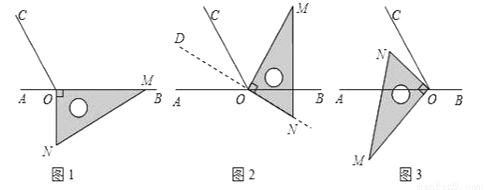
    （1）将图1中的三角板绕点O逆时针旋转至图2，使一边OM在∠BOC的内部，且恰好平分∠BOC．问：此时直线ON是否平分∠AOC？请说明理由．

    （2）将图1中的三角板绕点O以每秒10°的速度沿顺时针方向旋转一周，在旋转的过程中，第t秒时，直线ON恰好平分锐角∠AOC，则 t的值为 秒（直接写出结果）．

    （3）将图1中的三角板绕点O顺时针旋转至图3，使ON在∠AOC的内部，试探索：在旋转过程中，∠AOM与∠NOC的差是否发生变化？若不变，请求出这个差值；若变化，请求出差的变化范围．

    （1）直线ON平分∠AOC；（2）12或30秒；（3）差为定值30°． 【解析】试题分析：（1）直线ON平分∠AOC，设ON的反向延长线为OD，已知OM平分∠BOC，根据角平分线的定义可得∠MOC=∠MOB，又由OM⊥ON，根据垂直的定义可得∠MOD=∠MON=90°，所以∠COD=∠BON，再根据对顶角相等可得∠AOD=∠BON，即可∴∠COD=∠AOD，结论得证；（1）已知∠BOC=12...

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市2016-2017学年七年级上学期期末考试数学试卷 题型：解答题

    先化简，再求值．

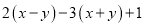    ，其中x=－1，y=.

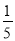    ，1． 【解析】试题分析：去括号、合并同类项后再代入求值即可. 试题解析： =2x-2y-3x-3y+1 =-x-5y+1 当x=－1，y=时，原式=1-1+1=1.

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市2016-2017学年七年级上学期期末考试数学试卷 题型：填空题

    在数轴上，表示与﹣3的点距离为5的数是_____．

    2或-8 【解析】在数轴上，表示与﹣3的点距离为5的数是-3+5=2或-3-5=-8．

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市2016-2017学年七年级上学期期末考试数学试卷 题型：单选题

    如图，田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分，发现剩下树叶的周长比原树叶的周长要小，能正确解释这一现象的数学知识是（ ）

    A. 垂线段最短

    B. 经过一点有无数条直线

    C. 经过两点，有且仅有一条直线

    D. 两点之间，线段最短

    D 【解析】试题解析：由图可知，剪掉一部分，相当于用一条线段取代了连接原来两点之间的曲线.根据线段公理：两点之间，线段最短，所以剩下树叶的周长比原树叶的周长要小. 故本题应选D.

    查看答案和解析>>

    科目：初中数学 来源：辽宁省葫芦岛市建昌县2017-2018学年八年级上学期期末测评数学试卷 题型：填空题

    数0.000 015用科学记数法表示为_______

    【解析】绝对值小于1的数由科学记数法表示时，指数由原数左边起第一个不为零的数字前面的0的个数所决定，故0.000 015=1.5×. 故答案为：

    查看答案和解析>>

    科目：初中数学 来源：2018年河南省驻马店市第一次中考模拟数学试卷 题型：解答题

    某园林专业户计划投资种植花卉及树木，根据市场调查与预测，种植树木的利润y1与投资量x成正比例关系，种植花卉的利润y2与投资量x的平方成正比例关系，并得到了表格中的数据．

    投资量x（万元）

    2

    种植树木利润y1（万元）

    4

    种植花卉利润y2（万元）

    2

    （1）分别求出利润y1与y2关于投资量x的函数关系式；

    （2）如果这位专业户以8万元资金投入种植花卉和树木，设他投入种植花卉金额m万元，种植花卉和树木共获利利润W万元，直接写出W关于m的函数关系式，并求他至少获得多少利润？他能获取的最大利润是多少？

    （3）若该专业户想获利不低于22万，在（2）的条件下，直接写出投资种植花卉的金额m的范围．

    （1）y1=2x（x≥0）；y2=x2（x≥0）；（2）他至少获得14万元利润，他能获取的最大利润是32万元；（3）6≤m≤8． 【解析】试题分析：（1）根据题意设y1=kx、y2=ax2，将表格中数据分别代入求解可得； （2）由种植花卉m万元（0≤m≤8），则投入种植树木（8-m）万元，根据“总利润=花卉利润+树木利润”列出函数解析式，利用二次函数的性质求得最值即可； （3）根据获利不...

    查看答案和解析>>

    同步练习册答案