练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图,已知△ABC的六个元素,则下列甲、乙、丙三个三角形中一定和△ABC全等的是(　　)

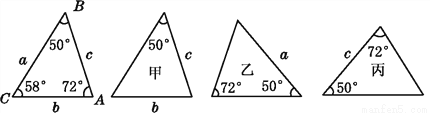
    A. 甲、乙 B. 甲、丙 C. 乙、丙 D. 乙

    C 【解析】【解析】 由图形可知，甲有一边一角，不能判断两三角形全等， 乙有两边及其夹角，能判断两三角形全等， 丙得出两角及其一角对边，能判断两三角形全等， 故乙丙正确．故选C．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：江苏省扬州市2017-2018学年八年级上学期期末考试数学试卷 题型：填空题

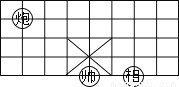
    如图，是象棋盘的一部分，若“帅”位于点（2，﹣1）上，“相”位于点（4，﹣1）上，则“炮”所在的点的坐标是________．

    (-1,2) 【解析】试题分析：根据“帅”位于点（2，-1）上，“相”位于点（4，-1）上，得：“炮”所在的点的坐标是（-1，2）．故答案为：（-1，2）．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018 北师大版七年级数学下册 第三章　变量之间的关系 单元测试卷 题型：填空题

    某种储蓄的月利率是0.2%，存入100元本金后，不扣除利息税，本息和y(元)与所存月数x(x为正整数)之间的关系为__________,4个月的本息和为________.

    y＝100＋0.2x 100.8元 【解析】第一个月y=100+100×0.2℅， 第二个月y=100+100×0.2℅+〔100+100×0.2℅〕×0.2℅ 结合题干可知y=100(1+0.2℅x)= y＝100＋0.2x， 令x=4,求得y=100.8. 故答案为： y＝100＋0.2x；100.8元.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.3.2 用“角边角、角角边”判定三角形全等 同步练习 题型：解答题

    如图①,在△ABC中,∠ACB=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于点M,BN⊥MN于点N.

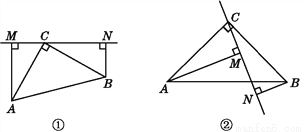
    (1)试说明:MN=AM+BN.

    (2)如图②,若过点C作直线MN与线段AB相交,AM⊥MN于点M,BN⊥MN于点N(AM>BN),(1)中的结论是否仍然成立?说明理由.

    (1) 答案见解析;(2) 不成立 【解析】试题分析：（1）利用互余关系证明∠MAC=∠NCB，又∠AMC=∠CNB=90°，AC=BC，故可证△AMC≌△CNB，从而有AM=CN，MC=BN，即可得出结论； （2）类似于（1）的方法，证明△AMC≌△CNB，从而有AM=CN，MC=BN，可推出AM、BN与MN之间的数量关系． 试题解析：解：（1）∵AM⊥MN，BN⊥MN，∴∠A...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.3.2 用“角边角、角角边”判定三角形全等 同步练习 题型：单选题

    根据图中所给条件,能够判定哪两个三角形全等?(　　)

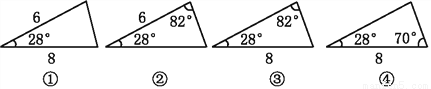
    A. ①和② B. ②和④

    C. ①和③ D. ③和④

    D 【解析】【解析】 ②中，第三个内角=180°－82°－28°=70°，③中，第三个内角=180°－82°－28°=70°，④中，第三个内角=180°－82°－28°=70°．故③和④中，根据ASA或AAS可判定两个三角形全等．故选D．

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级下册第三章3.2用关系式表示的变量间关系课时练习 题型：解答题

    在国内投寄平信应付邮资如下表：

    信件质量x（克）

    0＜x≤20

    0＜x≤40

    0＜x≤60

    邮资y（元）

    0.80

    1.60

    2.40

    ①y是x的函数吗？为什么？

    ②分别求当x=5，10，30，50时的函数值．

    y是x的函数； 0.80；0.80；1.60；2.40． 【解析】试题分析：①根据函数定义：设在一个变化过程中有两个变量x与y，对于x的每一个确定的值，y都有唯一的值与其对应，那么就说y是x的函数，x是自变量可得y是x的函数； ②根据表格可以直接得到答案． 试题解析：①y是x的函数，当x取定一个值时，y都有唯一确定的值与其对应； ②当x=5时，y=0.80； 当x=1...

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级下册第三章3.2用关系式表示的变量间关系课时练习 题型：单选题

    如图，梯形上底长、下底长分别是x，y，高是6，面积是24，则y与x之间的表达式是（　　）

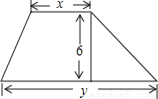
    A. y=﹣x+8 B. y=﹣x+4 C. y=x﹣8 D. y=x﹣4

    A 【解析】梯形上底长、下底长分别是x，y，高是6，面积是24， 则y与x之间的表达式是：24=（x+y）×6÷2， 即y=﹣x+8， 故选：A．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下册达标检测 第二章 相交线与平行线 题型：解答题

    将一副三角板拼成如图所示的图形，过点C作CF平分∠DCE交DE于点F．

    （1）求证：CF∥AB；

    （2）求∠DFC的度数．

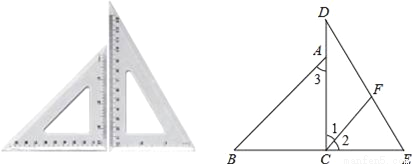
    （1）见解析；（2）105° 【解析】试题分析：（1）首先根据角平分线的性质可得∠1=45°，再有∠3=45°，再根据内错角相等两直线平行可判定出AB∥CF； （2）利用三角形内角和定理进行计算即可． 试题解析：（1）∵CF平分∠DCE，∴∠1=∠2=∠DCE，∵∠DCE=90°，∴∠1=45°，∵∠3=45°，∴∠1=∠3，∴AB∥CF（内错角相等，两直线平行）； （2）...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下6.2.1 频率的稳定性 同步练习 题型：单选题

    小明统计了他家今年5月份打电话的次数及通话时间,并列出了如下的频数分布表:

    通话时间

    x/min

    0<x≤5

    5<x≤10

    10<x≤15

    15<x≤20

    频数

    (通话次数)

    20

    16

    9

    5

    则通话时间不超过15 min的频率为(　　)

    A. 0.1 B. 0.4 C. 0.5 D. 0.9

    D 【解析】用不超过15分钟的通话时间除以所有的通话时间即可求得通话时间不超过15分钟的频率． 【解析】 ∵不超过15分钟的通话次数为20+16+9=45次，通话总次数为20+16+9+5=50次， ∴通话时间不超过15min的频率为=0.9， 故选D． “点睛”本题考查了频数分布表的知识，解题的关键是了解频率=频数÷样本容量，难度不大．

    查看答案和解析>>

    同步练习册答案