练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    不透明的口袋里装有红、黄、蓝三种颜色的小球若干个（除颜色外其余都相同），其中红球2个（分别标有1号、2号），蓝球1个．若从中任意摸出一个球，它是蓝球的概率为．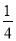

    （1）求袋中黄球的个数；

    （2）第一次任意摸出一个球（不放回），第二次再摸出一个球，请用画树状图或列表格的方法，求两次摸到不同颜色球的概率．

    （1）袋中黄球的个数为1个；（2）两次摸到不同颜色球的概率为：P=． 【解析】 试题分析:（1）首先设袋中黄球的个数为x个，由从中任意摸出一个球，它是蓝球的概率为，利用概率公式即可得方程： 解此方程即可求得答案；（2）首先根据题意画出树状图，然后由树状图求得所有等可能的结果与两次摸到不同颜色球的情况，再利用概率公式求解即可求得答案． 试题解析：（1）设袋中黄球的个数为x个， ∵从...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷（十） 题型：填空题

    如图，扇形OAB是圆锥的侧面展开图，若小正方形方格的边长为1cm，则这个圆锥的底面半径为_____．

    cm 【解析】用“此扇形的弧长等于圆锥底面周长”作为相等关系，求圆锥的底面半径． 【解析】 由图可知，OA=OB=，而AB=4，∴OA2+OB2=AB2，∴∠O=90°，OB==2； 则弧AB的长为==π，设底面半径r，则2πr=π，r=．这个圆锥的底面半径为cm． 故答案为： ． “点睛”圆锥的侧面展开图是一个扇形，此扇形的弧长等于圆锥底面周长，扇形的半径等于圆锥...

    查看答案和解析>>

    科目：初中数学 来源：山东省2017-2018学年七年级上期末模拟数学试卷 题型：解答题

    要加工200个零件，甲先单独加工了5小时，然后又与乙一起加工了4小时完成了任务．已知甲每小时比乙多加工2个零件，问甲、乙二人每小时各加工多少个零件？

    甲每小时加工16个零件，乙每小时加工14个零件． 【解析】试题分析：如果乙每小时加工x个零件，那么甲每小时加工（x+2）个零件，根据要加工200个零件，甲先单独加工5小时，然后又与乙一起加工4小时，完成了任务以及甲每小时比乙多加工2个，可列出方程求解即可． 试题解析：【解析】 设乙每小时加工x个零件，那么甲每小时加工（x+2）个零件．根据题意，列方程，得： 5（x+2）+4（x...

    查看答案和解析>>

    科目：初中数学 来源：山东省2017-2018学年七年级上期末模拟数学试卷 题型：单选题

    在一次数学实践探究活动中，大家遇到了这样的问题：

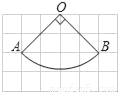
    如图，在一个圆柱体形状的包装盒的底部A处有一只壁虎，在顶部B处有一只小昆虫，壁虎沿着什么路线爬行，才能以最短的路线接近小昆虫？

    楠楠同学设计的方案是壁虎沿着A﹣C﹣B爬行；

    浩浩同学设计的方案是将包装盒展开，在侧面展开图上连接AB，然后壁虎在包装盒的表面上沿着AB爬行．

    在这两位同学的设计中，哪位同学的设计是最短路线呢？他们的理论依据是什么？（　　）

    A. 楠楠同学正确，他的理论依据是“直线段最短”

    B. 浩浩同学正确，他的理论依据是“两点确定一条直线”

    C. 楠楠同学正确，他的理论依据是“垂线段最短”

    D. 浩浩同学正确，他的理论依据是“两点之间，线段最短”

    D 【解析】【解析】 由题意可得：浩浩同学正确，他的理论依据是“两点之间，线段最短”．故选D．

    查看答案和解析>>

    科目：初中数学 来源：2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷（六） 题型：解答题

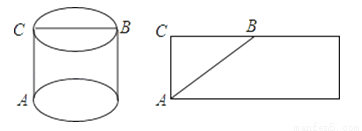
    已知，四边形ABCD是正方形，点P在直线BC上，点G在直线AD上（P、G不与正方形顶点重合，且在CD的同侧），PD=PG，DF⊥PG于点H，交直线AB于点F，将线段PG绕点P逆时针旋转90°得到线段PE，连结EF．

    （1）如图1，当点P与点G分别在线段BC与线段AD上时．

    ①求证：DG=2PC；

    ②求证：四边形PEFD是菱形；

    （2）如图2，当点P与点G分别在线段BC与线段AD的延长线上时，请猜想四边形PEFD是怎样的特殊四边形，并证明你的猜想．

    （1）①证明见解析；②证明见解析；（2）四边形PEFD是菱形．理由见解析． 【解析】试题分析：（1）①作PM⊥DG于M，根据等腰三角形的性质由PD=PG得MG=MD，根据矩形的判定易得四边形PCDM为矩形，则PC=MD，于是有DG=2PC； ②根据四边形ABCD为正方形得AD=AB，由四边形ABPM为矩形得AB=PM，则AD=PM，再利用等角的余角相等得到∠GDH=∠MPG，于是可根据...

    查看答案和解析>>

    科目：初中数学 来源：2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷（六） 题型：填空题

    如图，若BC∥DE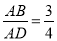， ，S△ABC=4，则四边形BCED的面积S四边形DBCE=_____．

    【解析】∵D、E分别是△ABC的AB、AC边上的点，DE∥BC， ∴△ADE∽△ABC， ∵AB：AD=3：4， ∴S△ABC：S△ADE=9：16， ∴S四边形DBCE：S△ABC=7：9， ∵△ABC的面积为4， ∴四边形DBCE的面积为． 故答案为： ．

    查看答案和解析>>

    科目：初中数学 来源：2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷（六） 题型：单选题

    某校开展“节约每一滴水”活动，为了了解开展活动一个月以来节约用水的情况，从八年级的400名同学中选取20名同学统计了各自家庭一个月约节水情况．见表：

    节水量/m3

    0.2

    0.25

    0.3

    0.4

    0.5

    家庭数/个

    2

    4

    6

    7

    1

    请你估计这400名同学的家庭一个月节约用水的总量大约是（　　）

    A. 130m3 B. 135m3 C. 6.5m3 D. 260m3

    A 【解析】试题分析：先计算这20名同学各自家庭一个月的节水量的平均数，即样本平均数，然后乘以总数400即可解答． 【解析】 20名同学各自家庭一个月平均节约用水是： （0.2×2+0.25×4+0.3×6+0.4×7+0.5×1）÷20=0.325（m3）， 因此这400名同学的家庭一个月节约用水的总量大约是： 400×0.325=130（m3）， 故选A．...

    查看答案和解析>>

    科目：初中数学 来源：甘肃省张掖市高台县2016-2017学年八年级（上）期末数学试卷 题型：填空题

    当m=______时，函数y=（2m﹣1）x3m﹣2是正比例函数．

    1． 【解析】试题解析：函数y=（2m﹣1）x3m﹣2是正比例函数． 解得： 故答案为：

    查看答案和解析>>

    科目：初中数学 来源：重庆市江北区2018届九年级上期末模拟数学试卷 题型：解答题

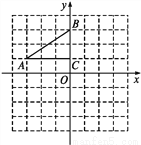
    如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,1),B(0,3),C(0,1).

    (1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;

    (2)分别连接AB1,BA1后,求四边形AB1A1B的面积.

    （1）画图见解析；（2）12 【解析】试题分析：（1）利用网格特点，延长AC到A1使A1C=AC，延长BC到B1使B1C=BC，C点的对应点C1与C点重合，则△A1B1C1满足条件； （2）四边形AB1A1B的对角线互相垂直平分，则四边形AB1A1B为菱形，然后利用菱形的面积公式计算即可． 试题解析：（1）如图，△A1B1C1为所作： （2）四边形AB1A1B的面积=×6×...

    查看答案和解析>>

    同步练习册答案