
如图,在△ABC中,AB>AC,点D、E分别是边AB、AC的中点,点F在BC边上,连接DE、DF、EF,则添加下列哪一个条件后,仍无法判断△FCE与△EDF全等( )

A. ∠A=∠DFE B. BF=CF C. DF∥AC D. ∠C=∠EDF
A 【解析】试题解析:A、∠A与∠CFE没关系,故A错误; B、BF=CF,F是BC中点,点D、E分别是边AB、AC的中点, ∴DF∥AC,DE∥BC, ∴∠CEF=∠DFE,∠CFE=∠DEF, 在△CEF和△DFE中 , ∴△CEF≌△DFE (ASA),故B正确; C、点D、E分别是边AB、AC的中点, ∴DE∥BC, ∴∠CFE=... 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案科目:初中数学 来源:北京八十五中2017-2018学年上期期末八年级数学试卷 题型:单选题
已知三角形两边长分别为7、11,那么第三边的长可以是( )
A. 2 B. 3 C. 4 D. 5
D 【解析】设第三边长为x,由题意得: 11﹣7<x<11+7, 解得:4<x<18, 故选:D.查看答案和解析>>
科目:初中数学 来源:2017年甘肃省平凉市中考数学模拟试卷 题型:填空题
关于x的一元二次方程kx2+2x﹣1=0有两个不相等的实数根,则k的取值范围是_____.
k>﹣1且k≠0. 【解析】∵一元二次方程kx²?2x?1=0有两个不相等的实数根, ∴△=b²?4ac=4+4k>0,且k≠0, 解得:k>?1且k≠0. 故答案为k>?1且k≠0.查看答案和解析>>
科目:初中数学 来源:2017年海南省定安县中考数学仿真试卷(二) 题型:解答题
如图,矩形ABCD中,AB=6,BC=8,E为AB上一点,且AE=2,M为AD上一动点(不与A、D重合),AM=x,连结EM并延长交CD的延长线于F,过M作MG⊥EF交直线BC于点G,连结EG、FG.
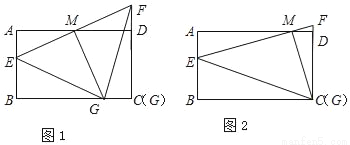
(1)如图1,若M是AD的中点,求证:①△AEM≌△DFM;②△EFG是等腰三角形;
(2)如图2,当x为何值时,点G与点C重合?
(3)当x=3时,求△EFG的面积.
(1)证明见解析(2)当x=2或6时,点G与点C重合(3) 【解析】试题分析:(1)①根据已知条件,利用ASA即可证得△AEM≌△DFM;②由△AEM≌△DFM可得EM=FM,又因MG⊥EF,根据线段垂直平分线的性质即可得EG=FG,结论得证;(2)当点G与点C重合时,易证△AEM∽△DMC,根据相似三角形的对应边成比例即可求得x值;(3)过G作GN⊥AD于N(如图3所示),证明△AEM∽△...查看答案和解析>>
科目:初中数学 来源:2017年海南省定安县中考数学仿真试卷(二) 题型:填空题
如果关于x的一元二次方程x2+4x﹣m=0没有实数根,那么m的取值范围是 .
m<﹣4 【解析】试题解析:∵一元二次方程x2+4x-m=0没有实数根, ∴△=16-4(-m)<0, ∴m<-4.查看答案和解析>>
科目:初中数学 来源:2017年海南省定安县中考数学仿真试卷(二) 题型:单选题
如图是若干个相同的小正方体组成的一个几何体的三视图,则小正方体的个数是( )
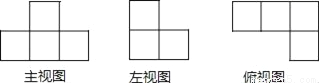
A. 3 B. 4 C. 5 D. 6
C 【解析】观察三视图,可得,这个几何体的底层应该有4个小正方体,第二层应该有1个小正方体, 因此搭成这个几何体的小正方体的个数为4+1=5个,故选C.查看答案和解析>>
科目:初中数学 来源:重庆市校2018届九年级上学期期末模拟数学试卷 题型:解答题
如图1,在△ACB和△AED中,AC=BC,AE=DE,∠ACB=∠AED=90°,点E在AB上,F是线段BD的中点,连接CE、FE.
(1)若AD=3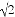 ,BE=4,求EF的长;
,BE=4,求EF的长;
(2)求证:CE=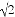 EF;
EF;
(3)将图1中的△AED绕点A顺时针旋转,使AED的一边AE恰好与△ACB的边AC在同一条直线上(如图2),连接BD,取BD的中点F,问(2)中的结论是否仍然成立,并说明理由.

查看答案和解析>>
科目:初中数学 来源:重庆市校2018届九年级上学期期末模拟数学试卷 题型:单选题
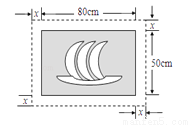
在一幅长80cm,宽50cm的矩形风景画的四周镶等宽的金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400 cm2,设金色纸边的宽为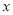 cm,根据题意所列方程正确的是( )
cm,根据题意所列方程正确的是( )
A. 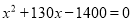 B.
B. 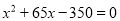
C. 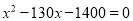 D.
D. 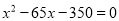
查看答案和解析>>
科目:初中数学 来源:江苏省东台市2017-2018学年上学期期末考试九年级数学试卷 题型:解答题
甲、乙、丙、丁四名同学进行一次乒乓球单打比赛,要从中选两位同学打第一场比赛.
(1)若由甲挑一名选手打第一场比赛,选中乙的概率是多少?(直接写出答案)
(2)任选两名同学打第一场,请用树状图或列表法求恰好选中甲、乙两位同学的概率。
(1) ;(2)见解析 【解析】试题分析:(1)直接利用概率公式求解; (2)画树状图展示所有12种等可能性结果数,再找出满足条件的结果数,然后根据概率公式求解. 试题解析:解:(1)∵共有乙、丙、丁三位同学,恰好选中乙同学的只有一种情况,∴P(恰好选中乙同学)=; (2)画树状图得: ∵所有出现的等可能性结果共有12种,其中满足条件的结果有2种. ∴P(恰好选...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com