
如图,△ABC中,∠A=46°,∠C=74°,BD平分∠ABC,交AC于点D,那么∠BDC的度数是( )
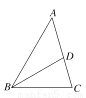
A. 76° B. 81° C. 92° D. 104°
A 【解析】根据三角形的内角和为180°,可得∠A+∠C+∠ABC=180°,然后根据△ABC中,∠A=46°,∠C=74°,求得∠ABC=60°,然后根据角平分线的性质,可得∠ABD=30°,再根据三角形的外角性质,可得∠BDC=∠A+∠ABD=76°. 故选:A.科目:初中数学 来源:北京大学附属中学2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
解不等式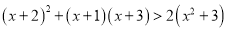 .
.
查看答案和解析>>
科目:初中数学 来源:浙江杭州萧山区高桥中学2017-2018学年七年级上学期期中数学试卷 题型:填空题
写出一个以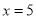 为解的一元一次方程__________.
为解的一元一次方程__________.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学人教版上册 第11章 三角形 单元测试卷 题型:解答题
如图,点E在AC上,点F在AB上,BE,CF交于点O,且∠C=2∠B,∠BFC-∠BEC=20°,求∠C的度数.
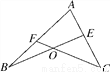
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学人教版上册 第11章 三角形 单元测试卷 题型:填空题
如图,在△ABC中,CD是AB边上的中线,E是AC的中点,已知△DEC的面积是4cm2,则△ABC的面积是______.
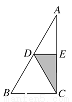
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学人教版上册 第11章 三角形 单元测试卷 题型:单选题
在四边形ABCD中,∠A=∠B=∠C,点E在边AB上,∠AED=60°,则一定有( )
A. ∠ADE=20° B. ∠ADE=30° C. ∠ADE=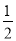 ∠ADC D. ∠ADE=
∠ADC D. ∠ADE=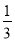 ∠ADC
∠ADC
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年七年级上学期期中考试数学试卷 题型:解答题
小兵喜欢研究数学问题,在计算整式的加减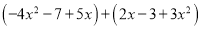 的时候,想到了小学的列竖式加减法,令
的时候,想到了小学的列竖式加减法,令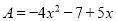 ,
, 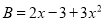 ,然后将两个整式关于
,然后将两个整式关于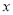 进行降幂排列,
进行降幂排列, 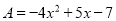 ,
, 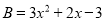 ,最后只要写出其各项系数对齐同类项进行竖式计算如下:
,最后只要写出其各项系数对齐同类项进行竖式计算如下:

所以, 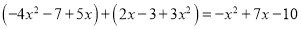
若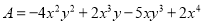 ,
, 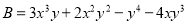 ,请你按照小兵的方法,
,请你按照小兵的方法,
先对整式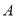 ,
, 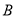 关于某个字母进行降幂排列,再写出其各项系数进行竖式计算
关于某个字母进行降幂排列,再写出其各项系数进行竖式计算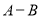 ,并写出
,并写出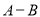 值.
值.
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年七年级上学期期中考试数学试卷 题型:单选题
如图,在一底面为长方形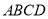 (长
(长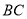 为
为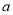 ,宽
,宽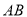 为
为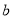 )的盒子底部,不重叠的放两张形状大小完全相同的两个长方形卡片,
)的盒子底部,不重叠的放两张形状大小完全相同的两个长方形卡片, 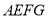 ,
, 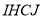 (长为
(长为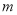 ,宽为
,宽为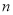 ),盒子底面未被卡片覆盖的部分用阴影表示,则图中两块阴影部分(长方形
),盒子底面未被卡片覆盖的部分用阴影表示,则图中两块阴影部分(长方形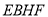 和
和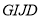 )的周长和是( ).
)的周长和是( ).

A. 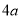 B.
B. 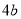 C.
C. 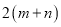 D.
D. 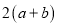
查看答案和解析>>
科目:初中数学 来源:浙江杭州拱墅区锦绣育才2017-2018学年七年级上学期期中数学 题型:填空题
关于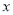 的方程
的方程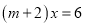 解为自然数,当
解为自然数,当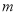 为整数时,则
为整数时,则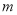 的值为__________.
的值为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com