
解方程:x+3-x(x+3)=0.(因式分解法)
x1=-3,x2=1. 【解析】x+3-x(x+3)=0. (x+3)(1-x)=0 x+3=0,1-x=0, x1=-3,x2=1.科目:初中数学 来源:江苏省2018届九年级12月月考数学试卷 题型:填空题
已知x=a是方程x2﹣6x+5=0的一个根,那么a2﹣6a=______.
-5. 【解析】【解析】 ∵x=a是方程x2﹣6x+5=0的一个根,∴a2﹣6a+5=0,∴a2﹣6a=-5.故答案为:-5.查看答案和解析>>
科目:初中数学 来源:人教版九年级数学上册经典试卷 第21章 一元二次方程韦达定理 测试卷 题型:解答题
已知关于x的方程x2-(2k+3)x+k2=0有两个不相等的实数根x1,x2.
(1)求k的取值范围;
(2)若两不相等的实数根满足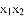 -
-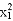 -
-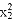 =-9,求实数k的值.
=-9,求实数k的值.
查看答案和解析>>
科目:初中数学 来源:人教版九年级数学上册经典试卷 第21章 一元二次方程韦达定理 测试卷 题型:单选题
已知关于x的方程(m-1)x2-2x+1=0有两个实数根,则m的取值范围是( ).
A. 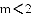
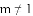
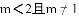
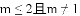
查看答案和解析>>
科目:初中数学 来源:人教版九年级数学上册经典试卷 第21章 一元二次方程韦达定理 测试卷 题型:单选题
如果关于x的方程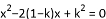 有实数根α、β,那么α+β的取值范围是( )
有实数根α、β,那么α+β的取值范围是( )
A. α+β≥1 B. α+β≤1 C. α+β≥ D. α+β≤
D. α+β≤
查看答案和解析>>
科目:初中数学 来源:天津市 2017-2018学年 九年级数学上册 一元二次方程 因式分解法 专题练习(含答案) 题型:解答题
解方程:x2+3x﹣4=0.(因式分解法)
x1=﹣4,x2=1. 【解析】因式分解可得:(x﹣1)(x+4)=0, ∴x﹣1=0或x+4=0, 解得:x1=﹣4,x2=1.查看答案和解析>>
科目:初中数学 来源:天津市 2017-2018学年 九年级数学上册 一元二次方程 因式分解法 专题练习(含答案) 题型:解答题
解方程:3x(x﹣2)=2(x﹣2).(因式分解法)
x1=2,x2=. 【解析】移项,得3x(x﹣2)﹣2(x﹣2)=0, 分解因式,得(x﹣2)(3x﹣2)=0, x-2=0,3x-2=0, 解得x1=2,x2=查看答案和解析>>
科目:初中数学 来源:天津市 2017-2018学年 九年级数学上册 一元二次方程 因式分解法 专题练习(含答案) 题型:填空题
方程x(x-2)=x的根是__________
x1=0,x2=3 【解析】x(x-2) -x=0. x(x-2-1)=0, x (x-3)=0, 所以x1=0,x2=3.查看答案和解析>>
科目:初中数学 来源:2017年甘肃省中考数学模拟试卷 题型:解答题
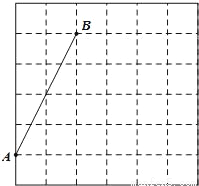
如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.
(1)在方格纸中画出以AB为一边的等腰△ABC,点C在小正方形的顶点上,且△ABC的面积为6.
(2)在方格纸中画出△ABC的中线BD,并把线段BD绕点C逆时针旋转90°,画出旋转后的线段EF(B与E对应,D与F对应),连接BF,请直接写出BF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com