练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若x2+2(m+1)x+25是一个完全平方式，那么m的值（ ）

    A. 4 或-6 B. 4 C. 6 或4 D. -6

    A 【解析】试题解析：∵x2+2（m+1）x+25是一个完全平方式， ∴△=b2-4ac=0， 即：[2（m+1）]2-4×25=0 整理得，m2+2m-24=0， 解得m1=4，m2=-6， 所以m的值为-2或8． 故选A.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：江苏省盐城市盐都区2017届九年级上学期期末考试数学试卷 题型：解答题

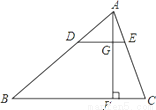
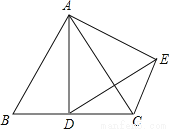
    如图，AF是△ABC的高，点D、E分别在AB、AC上，且DE∥BC，DE交AF于点G．设AD=5，AB=15，AC=12，GF=6．

    （1）求AE的长；

    （2）求点A到DE的距离AG的长．

    （1）AE=4；（2）AG=3． 【解析】分析：（1）证明△ADE∽△ABC，利用相似三角形的对应边的比相等即可求解； （2）证明△ADG∽△ABE，利用相似三角形的对应边的比相等即可求解． 本题解析： (1)∵DE∥BC， ∴△ADE∽△ABC， ∴,即， 解得AE=4； (2)∵DE∥BC， ∴△ADG∽△ABF， ∴,设AG=x,则...

    查看答案和解析>>

    科目：初中数学 来源：江苏省泰兴市2017-2018学年七年级上学期期末考试数学试卷 题型：填空题

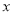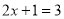    如果关于的方程和方程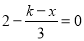的解相同，那么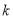的值为______．

    7 【解析】试题解析：∵2x+1=3 ∴x=1 又∵2-=0 即2-=0 ∴k=7． 故答案为：7

    查看答案和解析>>

    科目：初中数学 来源：河南省2017-2018学年八年级上学期期末考试数学试卷 题型：填空题

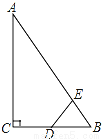
    如图，Rt△ABC中，∠ACB=90°，∠ABC=60°，BC=2cm，D为BC的中点，若动点E以1cm/s的速度从A点出发，沿着A→B的方向运动，设E点的运动时间为t秒（0≤t＜6），连接DE，当△BDE是直角三角形时，t的值为 ．

    2或3.5． 【解析】 试题分析：先求出AB的长，再分①∠BDE=90°时，DE是△ABC的中位线，然后求出AE的长度，再分点E在AB上和在BA上两种情况列出方程求解即可；②∠BED=90°时，利用∠B的余弦列式求出BE，列出方程求解即可． 【解析】 ∵∠ACB=90°，∠ABC=60°，BC=2cm， ∴AB=BC÷cos60°=2÷=4， ①∠BDE=90°时，...

    查看答案和解析>>

    科目：初中数学 来源：河南省2017-2018学年八年级上学期期末考试数学试卷 题型：单选题

    一个等腰三角形两边长分别为20和10，则周长为（ ）

    A. 40 B. 50 C. 40或50 D. 不能确定

    B 【解析】试题解析：①当10为腰时，10+10=20，故此种情况不存在； ②当20为腰时，20-10＜20＜20+10，符合题意． 故此三角形的周长=10+20+20=50． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：安徽省凤阳县梅市2017-2018学年九年级第一学期期末数学试卷 题型：解答题

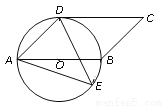
    如图，四边形ABCD是平行四边形，以AB为直径的⊙O经过点D，E是⊙O上一点，且∠AED=45?．

    (1)试判断CD与⊙O的位置关系，并证明你的结论；

    (2)若⊙O的半径为3，sin∠ADE=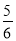，求AE的值．

    （1）CD与圆O相切，证明见解析；（2）AE=5 ． 【解析】（1）连接OD，则∠AOD=为直角，由四边形ABCD是平行四边形，则AB∥CD，从而得出∠CDO=90°，即可证出答案. （2）连接BE，则∠ADE=∠ABE，根据题意得sin∠ABE=. 由AB是圆O的直径求出AB的长.再在Rt△ABE中，求得AE即可. 【解析】 （1）CD与圆O相切． 证明：连接OD，则∠AOD...

    查看答案和解析>>

    科目：初中数学 来源：安徽省凤阳县梅市2017-2018学年九年级第一学期期末数学试卷 题型：填空题

    如图，在等边△ABC中，AB=6，D是BC的中点，将△ABD绕点A旋转后得到△ACE，那么线段DE的长度为 ．

    3． 【解析】 试题分析：首先，利用等边三角形的性质求得AD=；然后根据旋转的性质、等边三角形的性质推知△ADE为等边三角形，则DE=AD． 试题解析：如图，∵在等边△ABC中，∠B=60°，AB=6，D是BC的中点， ∴AD⊥BD，∠BAD=∠CAD=30°， ∴AD=ABcos30°=6×=3． 根据旋转的性质知，∠EAC=∠DAB=30°，AD=AE， ...

    查看答案和解析>>

    科目：初中数学 来源：北京市密云区2017-2018学年度第一学期期末考试初三数学试卷 题型：解答题

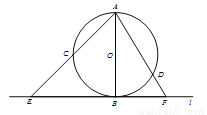
    如图，AB是⊙O的直径，C、D是⊙O上两点，弧AC=弧BC．过点B作⊙O的切线，连接AC并延长交于点E，连接AD并延长交于点F．

    （1）求证：AC=CE；

    （2）若AE=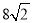，sin∠BAF= 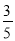，求DF长．

    （1）答案见解析；（2）． 【解析】试题分析：（1）连结BC，易证.由AB是的直径，EF切于点B，得，易得AB=BE，从而AC=CE； （2）通过解直角三角形即可. 试题解析：（1）证明：连结BC． AB是 的直径，C在上 AC=BC AB是的直径，EF切于点B AB=BE AC=CE （2）在中， ，AE= ，AB=BE 在中，AB=8...

    查看答案和解析>>

    科目：初中数学 来源：北京大兴区2017-2018学年度第一学期期末检测试卷 题型：填空题

    若△ABC∽△DEF，且BC∶EF=2∶3，则△ABC与△DEF的面积比等于__

    4∶9. 【解析】本题考查相似三角形的性质 若且其相似比为，则其面积之比为相似比的平方，即. 当△ABC∽△DEF，且对应边BC与EF的比为2∶3时，则△ABC与△DEF的面积之比为 故正确答案为

    查看答案和解析>>

    同步练习册答案