
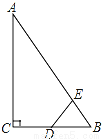
如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为 .
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源:河南省商丘市2017-2018学年上期七年级数学期末第一次模拟检测试卷 题型:单选题
若∠A=32°18′,∠B=32.18°,∠C=32.3°,则下列结论正确的是( )
A. ∠B=∠C B. ∠A=∠C C. ∠A=∠B D. ∠A=∠B
B 【解析】根据角度的换算,10°=60′,可知18′=0.3°,可知∠A=∠C. 故选:B.查看答案和解析>>
科目:初中数学 来源:江苏省泰兴市2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
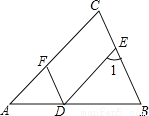
如图,∠AFD=∠1,AC∥DE.
(1)试说明:DF∥BC;
(2)若∠1=68°,DF平分∠ADE,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源:江苏省泰兴市2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
对于任何有理数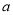 ,下列各式中一定为负数的是
,下列各式中一定为负数的是
A. 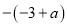 B.
B. 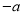 C.
C. 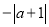 D.
D. 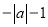
查看答案和解析>>
科目:初中数学 来源:河南省2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
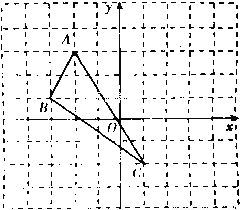
如图,在平面直角坐标系中,每个小正方形边长为1,点A的坐标为(-2,3)、点B的坐标为(-3,1)、点C的坐标为(1,-2)
(1)作出△ABC关于y轴对称的△A′B′C′(其中A′、B′、C′分别是A、B、C的对应点,不写画法).
(2) 直接写出A′、B′、C三点的坐标.
(3)在x轴上求作一点P,使PA+PB的值最小.(简要写出作图步骤)
查看答案和解析>>
科目:初中数学 来源:河南省2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
如图,在Rt△ABC中,∠CBA=90°,∠CAB的角平分线AP和∠ACB外角的平分线CF相交于点D,AD交CB于点P,CF交AB的延长线于点F,过点D作DE⊥CF交CB的延长线于点G,交AB的延长线于点E,连接CE并延长交FG于点H,则下列结论:①∠CDA=45°;②AF-CG=CA;③DE=DC;④FH=CD+GH;⑤CF=2CD+EG.其中正确的有( )
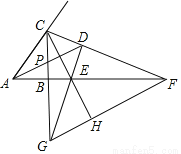
A. ①②④ B. ①②③ C. ①②④⑤ D. ①②③⑤
D 【解析】试题解析:①利用公式:∠CDA=∠ABC=45°,①正确; ②如图:延长GD与AC交于点P', 由三线合一可知CG=CP', ∵∠ADC=45°,DG⊥CF, ∴∠EDA=∠CDA=45°, ∴∠ADP=∠ADF, ∴△ADP'≌△ADF(ASA), ∴AF=AP'=AC+CP'=AC+CG,故②正确; ③如图: ∵∠EDA=...查看答案和解析>>
科目:初中数学 来源:河南省2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
若x2+2(m+1)x+25是一个完全平方式,那么m的值( )
A. 4 或-6 B. 4 C. 6 或4 D. -6
A 【解析】试题解析:∵x2+2(m+1)x+25是一个完全平方式, ∴△=b2-4ac=0, 即:[2(m+1)]2-4×25=0 整理得,m2+2m-24=0, 解得m1=4,m2=-6, 所以m的值为-2或8. 故选A.查看答案和解析>>
科目:初中数学 来源:安徽省凤阳县梅市2017-2018学年九年级第一学期期末数学试卷 题型:单选题
已知α是锐角,且点A(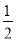 ,a),B(sin30°+cos30°,b), C(-m2+2m-2,c)都在二次函数y=-x2+x+3的图象上,那么a、b、c的大小关系是( )
,a),B(sin30°+cos30°,b), C(-m2+2m-2,c)都在二次函数y=-x2+x+3的图象上,那么a、b、c的大小关系是( )
A. a<b<c B. a<c<b C. b<c<a D. c<b<a
D 【解析】由题意可知抛物线的开口向下,对称轴是x= ,从而可知点A为抛物线的顶点,所以a最大,|sin30°+cos30°-| = ,|-m2+2m-2- |=(m-1)2+ ≥>,抛物线开口向下时离对称轴越近的点的y值越大,故b>c,所以c<b<a;故选D.查看答案和解析>>
科目:初中数学 来源:北京大兴区2017-2018学年度第一学期期末检测试卷 题型:解答题
已知:如图,ABCD是一块边长为2米的正方形铁板,在边AB上选取一点M,分别以AM和MB为边截取两块相邻的正方形板料. 当AM的长为何值时,截取两块相邻的正方形板料的总面积最小?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com