练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在平面直角坐标系xOy中，一次函数y=kx+b的图象与x轴相交于点A（－３，０），与y轴交于点B，且与正比例函数y=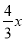的图象交点为C（m，4）求：

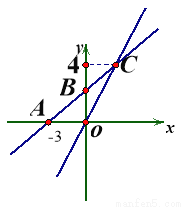
    （1）一次函数y=kx+b的解析式；

    （2）若点D在第二象限，△DAB是以AB为直角边的等腰直角三角形，直接写出点D的坐标。

    （3）在x轴上求一点P使△POC为等腰三角形，请直接写出所有符合条件的点P的坐标．

    （1） ;（2） （-2，5）或（-5，3）．（3） （5，0）或（-5，0）或（6，0）或（，0）． 【解析】 试题分析：（1）首先利用待定系数法把C（m，4）代入正比例函数y=中，计算出m的值，进而得到C点坐标，再利用待定系数法把A、C两点坐标代入一次函数y=kx+b中，计算出k、b的值，进而得到一次函数解析式． （2）利用△BED1≌△AOB，△BED2≌△AOB，即可得出...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版数学七年级上册 第四章 基本平面图形练习题 题型：单选题

    下列说法正确的是( )

    A. 两点之间直线最短

    B. 画出A，B两点间的距离

    C. 连接点A与点B的线段，叫A，B两点间的距离

    D. 两点之间的距离是一个数，不是指线段本身

    D 【解析】解：A． 两点之间线段最短，故A错误； B． 量出A，B两点间的距离，故B错误； C． 连接点A与点B的线段的长，叫A，B两点间的距离，故C错误； D． 两点之间的距离是一个数，不是指线段本身，正确． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：2018年春人教版七年级数学下册期中测试 题型：单选题

    如图，直线a，b被直线c所截，下列条件能判断a∥b的是（　　）

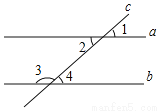
    A. ∠1=∠2 B. ∠1=∠4

    C. ∠3+∠4=180° D. ∠2=30°，∠4=35°

    B 【解析】∠1＝∠4, a∥b,同位角相等，两直线平行.选B.

    查看答案和解析>>

    科目：初中数学 来源：山东省诸城市2018届九年级上期末模拟数试卷 题型：填空题

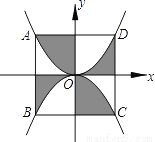
    如图，边长为2的正方形ABCD的中心在直角坐标系的原点O，AD∥x轴，以O为顶点且过A、D两点的抛物线与以O为顶点且过B、C两点的抛物线将正方形分割成几部分．则图中阴影部分的面积是________．

    2 【解析】：根据图示及抛物线、正方形的性质，S阴影=S正方形=×2×2=2．故答案为：2

    查看答案和解析>>

    科目：初中数学 来源：山东省诸城市2018届九年级上期末模拟数试卷 题型：单选题

    已知三点P1（x1 ， y1），P2（x2 ， y2），P3（x3 ， y3）都在反比例函数y=-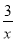的图象上，若x1＜0＜x2＜x3， 则下列式子正确的是（　　）

    A. y1＜y2＜y3 B. y3＜y2＜y1 C. y2＞y3＞y1 D. y1＞y3＞y2

    D 【解析】试题分析：：∵反比例函数y＝中k＝－3＜0， ∴函数图象在二四象限，在每一个象限内y随x的增大而增大， ∵x1＜0＜x2＜x3， ∴点P1（x1，y1）在第二象限，y1＞0，点P2（x2，y2），P3（x3，y3）在第四象限， ∴y1＞y3＞y2． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：江苏省盐城市2017-2018学年八年级12月月考数学试卷 题型：解答题

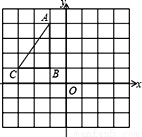
    如图，在直角坐标系中，Rt△ABC三个顶点均在边长为1的正方形网格格点上．

    （1）作出△ABC关于y轴对称的△A′B′C′；

    （2）若在y轴上有点 D（0,2），在所给的网格中的格点上，以A、C、D、E为顶点的四边形为平行四边形，请在图中标出点E，并直接写出点E的坐标．

    （1）见解析；（2）（2.5），（-4,3），（-2，-1） 【解析】试题分析：（1）分别作出点A、B、C关于y轴对称的点，然后顺次连接； （2）根据平行四边形的判定找出D点位置即可，不要漏解． 【解析】 （1）如图所示： （2）（2.5），（-4,3），（-2，-1）

    查看答案和解析>>

    科目：初中数学 来源：江苏省盐城市2017-2018学年八年级12月月考数学试卷 题型：填空题

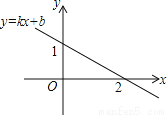
    已知一次函数y=kx+b的图象如图，则y＞1时x的取值范围是_________．

    x＜0 【解析】由图像可知，当x＜0时，y＞1， ∴y＞1时x的取值范围是：x＜0.

    查看答案和解析>>

    科目：初中数学 来源：甘肃省定西市安定区2016-2017学年八年级上学期期末考试数学试卷 题型：解答题

    先化简，再求值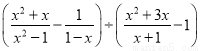： ，其中x＝2．

    ， 【解析】试题分析：先算括号里面的，再算除法，最后把x的值代入进行计算即可． 试题解析：原式= = = = =， 当x=2时，原式=．

    查看答案和解析>>

    科目：初中数学 来源：山东省滨州市部2017-2018学年八年级（上）第一次月考数学试卷 题型：单选题

    对于任意三角形的高，下列说法不正确的是（ ）

    A. 锐角三角形有三条高 B. 直角三角形只有一条高

    C. 任意三角形都有三条高 D. 钝角三角形有两条高在三角形的外部

    B 【解析】试题分析：根据三角形的高的概念，通过具体作高，发现：任意一个三角形都有三条高，其中锐角三角形的三条高都在三角形的内部；直角三角形有两条高即三角形的两条直角边，一条在内部；钝角三角形有两条高在三角形的外部，一条在内部，据此可知： A、锐角三角形有三条高，说法正确，故本选项不符合题意； B、直角三角形有三条高，说法错误，故本选项符合题意； C、任意三角形都有三条高，...

    查看答案和解析>>

    同步练习册答案