
��ͼ��AB�ǡ�O��ֱ������AB =6��C�ǡ�O��һ�㣬D��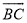 ���е㣬����D����O�����ߣ���AB��AC���ӳ��߷ֱ��ڵ�E��F������AD.
���е㣬����D����O�����ߣ���AB��AC���ӳ��߷ֱ��ڵ�E��F������AD.
(l)��֤��AF��EF;
(2)��գ�
�ٵ�BE= ʱ����C��AF���е㣻
�ڵ�BE= ʱ���ı���OBDC�����Σ�
��1��֤������������2����6����3 �������������������1������OD����ֱ��EF�� O�����ڵ�D���õ�OD��EF����ͬԲ�İ뾶����Ƴ���1=��3���ɵ�DΪ���е㣬�õ���1=��2��֤�á�2=��3���õ�OD��AF���ó�����AF��EF����2���ٸ���ƽ���߷��߶γɱ�����������BΪ��AE�е�ʱ����C��AF���е㣻�������ߵ����ʿ�֤��OD��EF������ֱ��������б���ϵ����ߵ����ʵõ�BD=OB=BE, ... ������ÿ�ʱ�Ż���ҵϵ�д�
������ÿ�ʱ�Ż���ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ�»���2016-2017ѧ��ȵڶ�ѧ�����м�����꼶��ѧ�Ծ� ���ͣ������
��ʽ�֡�������
2a2 �C 8 = _______________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ̩����2017���п���ѧ��ģ�Ծ��������棩 ���ͣ������
��ͼ����ABC�ڽ��ڡ�O��BDΪ��O��ֱ����BD��AC�ཻ�ڵ�H��AC���ӳ��������B��ֱ���ཻ�ڵ�E���ҡ�A=��EBC��
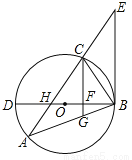
��1����֤��BE�ǡ�O�����ߣ�
��2����֪CG��EB����CG��BD��BA�ֱ��ཻ�ڵ�F��G����BG•BA=48��FG=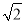 ��DF=2BF����AH��ֵ��
��DF=2BF����AH��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ̩����2017���п���ѧ��ģ�Ծ��������棩 ���ͣ������
��ͳ�ƣ��μӽ��������г��б�ҵ����ѧͳһ���Ե�ѧ��Լ36800�ˣ���������ÿ�ѧ��������ʾΪ_________��
3.68��104 �������� .�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�п���ѧ��ģ�Ծ� ���ͣ������
��ͼ����֪������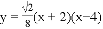 ��x�ύ�ڵ�A��B����Aλ�ڵ�B��ࣩ����y�ύ�ڵ�C��CD��x�ύ�������ڵ�D��MΪ�����ߵĶ��㣮
��x�ύ�ڵ�A��B����Aλ�ڵ�B��ࣩ����y�ύ�ڵ�C��CD��x�ύ�������ڵ�D��MΪ�����ߵĶ��㣮
��1�����A��B��C�����ꣻ
��2���趯��N��-2��n������ʹMN+BN��ֵ��Сʱn��ֵ��
��3��P����������λ��x���Ϸ���һ�㣬��̽�����Ƿ���ڵ�P��ʹ��P��A��BΪ��������������ABD���ƣ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�п���ѧ��ģ�Ծ� ���ͣ������
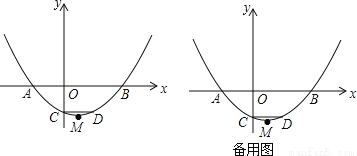
��ͼ��A��B�Ƿ��������� ͼ���ϵ����㣬����A��AC��y�ᣬ����ΪC��AC��OB�ڵ�D����DΪOB���е㣬��AOD�����Ϊ3����k��ֵΪ_____��
ͼ���ϵ����㣬����A��AC��y�ᣬ����ΪC��AC��OB�ڵ�D����DΪOB���е㣬��AOD�����Ϊ3����k��ֵΪ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�п���ѧ��ģ�Ծ� ���ͣ���ѡ��
����������y=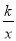 ��k��0��ͼ���ϵ�������A��x1,y1����B��x2,y2������x1<x2<0ʱ��y1>y2����ôһ�κ���y= -2kx +k��ͼ������ ��
��k��0��ͼ���ϵ�������A��x1,y1����B��x2,y2������x1<x2<0ʱ��y1>y2����ôһ�κ���y= -2kx +k��ͼ������ ��
A. ��һ���� B. �ڶ����� C. �������� D. ��������
C ���������ߵ�x1�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭�������������m��ʵ��ѧУ2018����꼶��ѧ�����п�����ѧ�Ծ����������� ���ͣ������
��ͼ���ڡ� �У���
����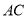 ��
�� 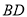 �ཻ�ڵ�
�ཻ�ڵ�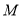 ����
���� ��
��
��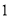 ����֤��
����֤�� 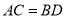 ��
��
��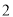 ����
����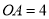 ��
�� 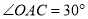 ����
����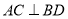 ʱ����
ʱ����
��ͼ����Ӱ���������
�ڻ� �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ2017-2018ѧ����꼶12���¿���ѧ�Ծ� ���ͣ���ѡ��
������������ȷ����ĸ����� �� ��
��3��ƽ������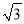 �� ��-3��9��ƽ������ ��
�� ��-3��9��ƽ������ ��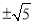 ����5��ƽ������ �ܸ���û����������
����5��ƽ������ �ܸ���û����������
A. 1�� B. 2�� C. 3�� D. 4��
B ����������Ϊ3��ƽ������,���Ԣٴ���, ��Ϊ��3��9��ƽ����,���Ԣ���ȷ,��Ϊ����5��ƽ����,���Ԣ���ȷ,��Ϊ������������,���Ԣܴ���,��ѡB.�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com