
如图所示,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )

A. 三角形的稳定性 B. 两点之间线段最短 C. 两点确定一条直线 D. 垂线段最短
A 【解析】试题分析:窗户打开后,用窗钩钩住,正好构成三角形的形状,因此可以将其固定,主要利用了三角形的稳定性.故选A. 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源:浙江杭州西湖区保俶塔实验学校2018届九年级上学期期中考试数学试卷(含解析) 题型:解答题
如图,在平面直角坐标系中,抛物线 与
与 轴交与点
轴交与点 ,与
,与 轴交于
轴交于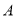 、
、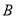 两点,点
两点,点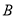 坐标为
坐标为 ,抛物线的对称轴方程为
,抛物线的对称轴方程为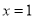 .
.
(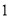 )求抛物线的解析式.
)求抛物线的解析式.
( )点
)点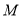 从
从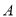 点出发,在线段
点出发,在线段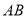 上以每秒
上以每秒 个单位长度的速度向
个单位长度的速度向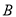 点运动,同时点
点运动,同时点 从
从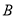 点出发,在线段
点出发,在线段 上以每秒
上以每秒 个单位长度的速度向
个单位长度的速度向 点运动,其中一个点到达终点时,另一个点也停止运动,在点
点运动,其中一个点到达终点时,另一个点也停止运动,在点 运动过程中,是否存在某一时刻
运动过程中,是否存在某一时刻 ,使
,使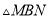 为直角三角形?若存在,求出
为直角三角形?若存在,求出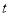 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
( )若点
)若点 为抛物线对称轴上一点,当
为抛物线对称轴上一点,当 是直角三角形时,求点
是直角三角形时,求点 的坐标.
的坐标.
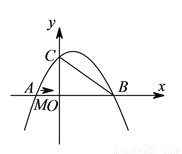
查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年八年级12月月考数学试卷 题型:单选题
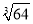 的算术平方根是( )
的算术平方根是( )
A. 4 B. ±4 C. 2 D. ±2
C 【解析】因为=4,4的算术平方根是2,所以的算术平方根是2,故选C.查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2017-2018学年八年级上册期末模拟数学试卷 题型:填空题
直线x+2y=5与直线x+y=3的交点坐标是________.
(1,2) 【解析】联立两个函数解析式, 解得: ,则交点坐标为(1,2), 故答案为:(1,2).查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2017-2018学年八年级上册期末模拟数学试卷 题型:单选题
如图,直线y=kx+b交坐标轴于A(﹣3,0)、B(0,1)两点,则不等式﹣kx﹣b<0的解集为( )
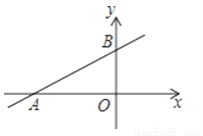
A. x>﹣3 B. x<﹣3 C. x>3 D. x<3
A 【解析】求﹣kx﹣b<0的解集,即为kx+b>0,就是求函数值大于0时,x的取值范围为:当y>0时,x>﹣3. 故选:A.查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2017-2018学年八年级上册期末模拟数学试卷 题型:解答题
如图,已知,l1∥l2 , C1在l1上,并且C1A⊥l2 ,A为垂足,C2, C3是l1上任意两点,点B在l2上.设△ABC1的面积为S1, △ABC2的面积为S2, △ABC3的面积为S3, 小颖认为S1=S2=S3, 请帮小颖说明理由.
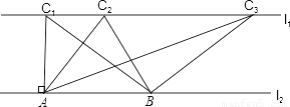
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2017-2018学年八年级上册期末模拟数学试卷 题型:填空题
用不等号“>、<、≥、≤”填空:a2+1 0.
> 【解析】 试题解析:根据a2≥0, ∴a2+1>0.查看答案和解析>>
科目:初中数学 来源:湖南省邵阳县黄亭市2017~2018学年九年级数学(上)期末综合检测模拟题 题型:解答题
某中学组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示:

(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价应定为多少元?
(1)y是x的反比例函数,;(2)240. 【解析】 试题分析:(1)由表中数据得出xy=6000,即可得出结果; (2)由题意得出方程,解方程即可,注意检验. 试题解析:(1)由表中数据得:xy=6000,∴,∴y是x的反比例函数,故所求函数关系式为; (2)由题意得:(x﹣120)y=3000,把代入得:(x﹣120)•=3000,解得:x=240; 经检验...查看答案和解析>>
科目:初中数学 来源:2017年甘肃省兰州市中考数学模拟试卷 题型:单选题
某城市2014年底已有绿化面积300公顷,经过两年绿化,绿化面积逐年增加,到2016年底增加到363公顷,设绿化面积平均每年的增长率为x,由题意,所列方程正确的是( )
A. 300(1+x)=363 B. 300(1+x)2=363 C. 300(1+2x)=363 D. 363(1-x)2=300
B 【解析】试题分析:知道2004年的绿化面积经过两年变化到2006,绿化面积成为363,设绿化面积平均每年的增长率为x,由题意可列出方程. 【解析】 设绿化面积平均每年的增长率为x, 300(1+x)2=363. 故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com