
如图,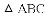
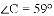
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:人教版八年级数学 第十二章 全等三角形 检测题(附答案) 题型:填空题
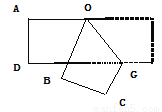
把一张长方形纸条按如图所示折叠得到∠AOB=70°,则∠BOG=______.
查看答案和解析>>
科目:初中数学 来源:北师大版(贵州)八年级数学下册:期末综合检测 题型:填空题
一元一次不等式组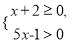 的解集是 .
的解集是 .
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区第十三中学2017-2018学年八年级上学期中考试数学试卷(含解析) 题型:解答题
(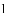
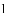
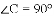
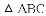
(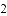
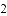
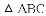
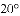
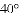
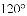
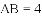
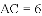
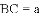
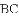
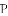

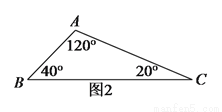


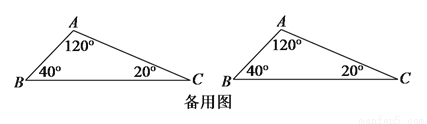
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区第十三中学2017-2018学年八年级上学期中考试数学试卷(含解析) 题型:填空题
如图,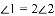
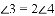
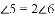
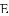
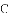
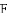
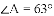
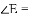
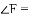
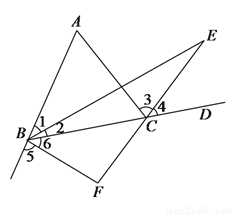
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区第十三中学2017-2018学年八年级上学期中考试数学试卷(含解析) 题型:单选题
如图,在四边形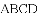
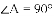
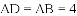
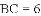
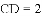
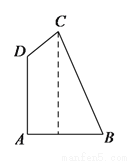
A. 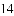
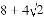 C.
C. 
查看答案和解析>>
科目:初中数学 来源:2017年内蒙古呼和浩特市中考数学试卷六 题型:解答题
某校初三年级学生参加赈灾义演活动,甲班捐款200元,乙班30名同学捐款200元,这样,两班人均捐款比甲班人均捐款多1元,甲班有多名学生参加这次赈灾活动?(规定班级人数不超过60人)
50 【解析】试题分析:本题先根据题意得出等量关系即两班人均捐款比甲班人均捐款多1元,从而列出方程得 解出方程,最后检验并作答. 试题解析:设甲班有名同学参加这次赈灾活动. 根据题意,得 去分母,整理,得 解得: 经检验,均为原方程的根, 不合题意,舍去. 答:甲班有50名同学参加这次赈灾活动.查看答案和解析>>
科目:初中数学 来源:2017年内蒙古呼和浩特市中考数学试卷六 题型:单选题
某商店有两个进价不同的计算器都卖了64元,其中一个盈利60%,另一个亏损20%,在这次买卖中,这家商店( )
A. 不赔不赚 B. 赚了32元 C. 赔了8元 D. 赚了8元
D 【解析】试题分析:要计算赔赚,就要分别求出两个计算器的进价,再与售价作比较即可.因此就要先设出未知数,根据进价+利润=售价,利用题中的等量关系列方程求解. 【解析】 设盈利60%的进价为x元, 则:x+60%x=64, 解得:x=40, 再设亏损20%的进价为y元,则; y﹣20%y=64, 解得:y=80, 所以总进价是120元,总售价是12...查看答案和解析>>
科目:初中数学 来源:江苏省无锡市江阴市要塞片2017-2018学年七年级(上)期中数学模拟试卷 题型:填空题
长为7个单位长度的木条放在数轴上,最少能覆盖_____个表示整数的点,最多能覆盖_____个表示整数的点.
7 8 【解析】如图所示,长为7个单位长度的木条放在数轴上,最少能覆盖7个表示整数的点,最多能覆盖8个表示整数的点, 故答案为:7,8.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com