
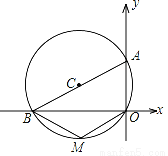
如图,⊙C过原点O,且与两坐标轴分别交于点A、B,点A的坐标为(0,2),M是第三象限内⊙C上一点,∠BMO=120°,则圆心C的坐标为( )
A. (1,1) B. (1, 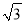 ) C. (2,1) D. (﹣
) C. (2,1) D. (﹣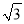 ,1)
,1)
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2016-2017学年黑龙江省哈尔滨市松北区2017届九年级上学期期末数学试卷 题型:解答题
为便于管理与场地安排,松北某中学校以小明所在班级为例,对学生参加各个体育项目进行了调查统计.并把调查的结果绘制了如图所示的不完全统计图,请你根据下列信息回答问题:
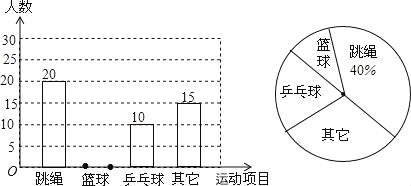
(1)在这次调查中,小明所在的班级参加篮球项目的同学有多少人?并补全条形统计图.
(2)如果学校有800名学生,请估计全校学生中有多少人参加篮球项目.
(1)5人,画图见解析.(2)80人; 【解析】 试题分析:(1)根据跳绳人数除以跳绳人数所占的百分比,可得抽查总人数,根据有理数的减法,可得参加篮球项目的人数,根据参加篮球项目的人数,可得答案; (2)根据全校学生人数乘以参加篮球项目所占的百分比,可得答案. 试题解析:(1)抽查总人数是:20÷40%=50(人), 参加篮球项目的人数是:50﹣20﹣10﹣15=5(...查看答案和解析>>
科目:初中数学 来源:黑龙江省密山市2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
下列命题:①有一个外角是120°的等腰三角形是等边三角形;②全等的两个三角形一定关于某条直线对称;③等腰三角形的高线、中线、角平分线互相重合;④圆是轴对称图形,有无数条对称轴,直径就是它的对称轴。其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
A 【解析】①因为外角和与其对应的内角的和是180°,已知有一个外角是120°,即是有一个内角是60°,有一个内角为60°的等腰三角形是等边三角形,①正确;②全等的两个三角形不一定关于某条直线对称,②错误;③等腰三角形底边上的高线、中线、顶角的角平分线互相重合,③错误;④圆是轴对称图形,有无数条对称轴,每一条直径所在的直线都是它的对称轴,④错误.故选A.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷(C卷) 题型:填空题
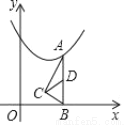
如图,在平面直角坐标系中,点A在抛物线y=x2﹣2x+3上运动,过点A作AB⊥x轴于点B,以AB为斜边作Rt△ABC,则AB边上的中线CD的最小值为______.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷(C卷) 题型:单选题
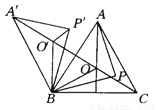
如图所示,O是锐角三角形ABC内一点,∠AOB=∠BOC=∠COA=120°,P是△ABC内不同于O的另一点,△A′BO′、△A′BP′分别由△AOB、△APB旋转而得,旋转角都为60°,则下列结论中正确的有( ).(提示:有一个角是60°的等腰三角形是等边三角形)
①△O′BO为等边三角形,且A′、O′、O、C在一条直线上.
②A′O′+O′O=AO+BO. ③A′P′+P′P=PA+PB.
④PA+PB+PC>AO+BO+CO.
A. 1个 B. 2个 C. 3个 D. 4个
D 【解析】【解析】 连PP′,如图,∵△A′BO′,△A′BP′分别由△AOB,△APB旋转而得,旋转角都为60°,∴BO′=BO,BP′=BP,∠OBO′=∠PBP′=60°,∠A′O′B=∠AOB,O′A′=OA,P′A′=PA,∴△BOO′和△BPP′都是等边三角形,∴∠BOO′=∠BO′O=60°,OO′=OB,而∠AOB=∠BOC=∠COA=120°,∴∠A′O′O=∠O′OC...查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷(A卷) 题型:解答题
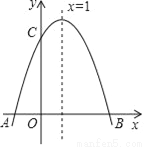
如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,交y轴于C点,其中B点坐标为(3,0),C点坐标为(0,3),且图象对称轴为直线x=1.
(1)求此二次函数的关系式;
(2)P为二次函数y=ax2+bx+c图象上一点,且S△ABP=S△ABC,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷(A卷) 题型:解答题
解下列方程
(1)(x﹣3)2=3﹣x; (2)2x2+1=4x.
(1), ;(2), . 【解析】试题分析:第小题用因式分解法,第小题用公式法. 试题解析:(1)原方程, 或, , . (2)原方程, . , .查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷(A卷) 题型:单选题
用配方法解方程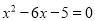 ,下列配方结果正确的是( )
,下列配方结果正确的是( )
A. 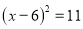 B.
B. 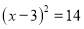 C.
C. 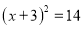 D.
D. 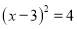
查看答案和解析>>
科目:初中数学 来源:广西南宁市2017年中考数学一模试卷 题型:单选题
如图,直线y=x+4与双曲线y=﹣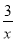 相交于A、B两点,点P是y轴上的一个动点,当PA+PB的值最小时,点P的坐标为( )
相交于A、B两点,点P是y轴上的一个动点,当PA+PB的值最小时,点P的坐标为( )
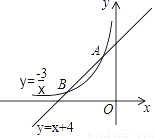
A. (0, 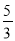 ) B. (0,
) B. (0, 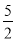 ) C. (0,﹣
) C. (0,﹣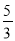 ) D. (0,﹣
) D. (0,﹣ 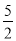 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com