
(本题满分6分)
求证:对角线互相垂直的平行四边形是菱形.
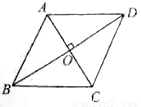
小红同学根据题意画出了图形,并写出了已知和求证的一部分,请你补全已知和求证,并写出证明过程.
已知:如图,在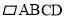 中,对角线
中,对角线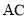 ,
,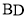 交于点
交于点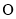 , .
, .
求证: .
科目:初中数学 来源:2017年初中毕业升学考试(湖北荆门卷)数学(解析版) 题型:填空题
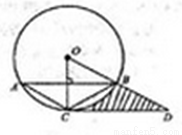
已知:如图,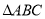 内接于
内接于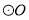 ,且半径
,且半径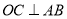 ,点
,点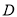 在半径
在半径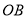 的延长线上,且
的延长线上,且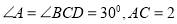 ,则由
,则由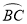 ,线段
,线段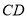 和线段
和线段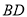 所围成图形的阴影部分的面积为____________.
所围成图形的阴影部分的面积为____________.
查看答案和解析>>
科目:初中数学 来源:2017年初中毕业升学考试(湖南张家界卷)数学(解析版) 题型:解答题
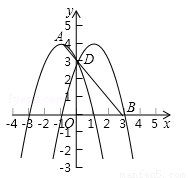
已知抛物线c1的顶点为A(﹣1,4),与y轴的交点为D(0,3).
(1)求c1的解析式;
(2)若直线l1:y=x+m与c1仅有唯一的交点,求m的值;
(3)若抛物线c1关于y轴对称的抛物线记作c2,平行于x轴的直线记作l2:y=n.试结合图形回答:当n为何值时,l2与c1和c2共有:①两个交点;②三个交点;③四个交点;
(4)若c2与x轴正半轴交点记作B,试在x轴上求点P,使△PAB为等腰三角形.
查看答案和解析>>
科目:初中数学 来源:2017年初中毕业升学考试(湖南张家界卷)数学(解析版) 题型:选择题
如图是一个正方体的表面展开图,则原正方体中与“美”字所在面相对的面上标的字是( )
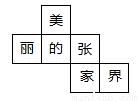
A.丽 B.张 C.家 D.界
查看答案和解析>>
科目:初中数学 来源:2017年初中毕业升学考试(湖南岳阳卷)数学(解析版) 题型:解答题
(本题满分10分)
问题背景:已知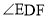 的顶点
的顶点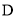 在
在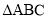 的边
的边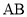 所在直线上(不与
所在直线上(不与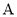 ,
,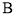 重合).
重合).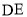 交
交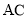 所在直线于点
所在直线于点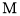 ,
,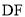 交
交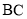 所在直线于点
所在直线于点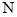 .记
.记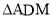 的面积为
的面积为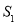 ,
,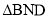 的面积为
的面积为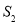 .
.
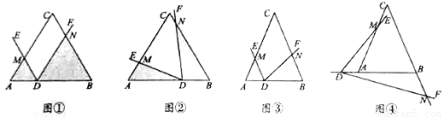
(1)初步尝试:如图①,当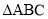 是等边三角形,
是等边三角形,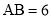 ,
,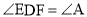 ,且
,且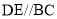 ,
,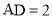 时,则
时,则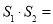 ;
;
(2)类比探究:在(1)的条件下,先将点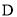 沿
沿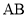 平移,使
平移,使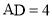 ,再将
,再将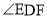 绕点
绕点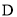 旋转至如图②所示位置,求
旋转至如图②所示位置,求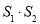 的值;
的值;
(3)延伸拓展:当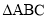 是等腰三角形时,设
是等腰三角形时,设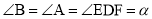 .
.
(I)如图③,当点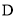 在线段
在线段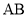 上运动时,设
上运动时,设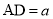 ,
,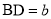 ,求
,求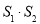 的表达式(结果用
的表达式(结果用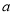 ,
,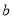 和
和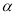 的三角函数表示).
的三角函数表示).
(II)如图④,当点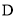 在
在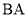 的延长线上运动时,设
的延长线上运动时,设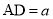 ,
,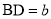 ,直接写出
,直接写出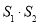 的表达式,不必写出解答过程.
的表达式,不必写出解答过程.
查看答案和解析>>
科目:初中数学 来源:2017年初中毕业升学考试(湖南永州卷)数学(解析版) 题型:填空题
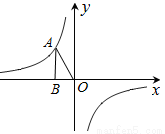
如图,已知反比例函数y=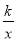 (k为常数,k≠0)的图象经过点A,过A点作AB⊥x轴,垂足为B,若△AOB的面积为1,则k=________________.
(k为常数,k≠0)的图象经过点A,过A点作AB⊥x轴,垂足为B,若△AOB的面积为1,则k=________________.
查看答案和解析>>
科目:初中数学 来源:2017年初中毕业升学考试(湖南怀化卷)数学(解析版) 题型:解答题
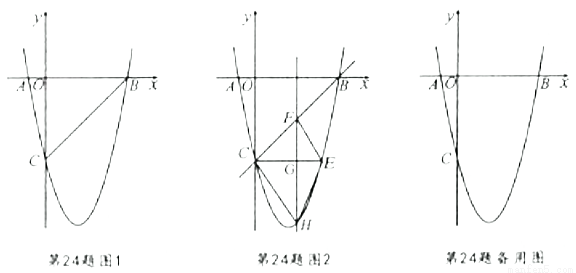
如图1,在平面直角坐标系中,已知抛物线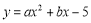 与
与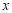 轴交于
轴交于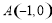 ,
,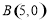 两点,与
两点,与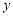 轴交于点
轴交于点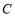 .
.
(1)求抛物线的函数表达式;
(2)若点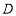 是
是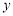 轴上的一点,且以
轴上的一点,且以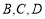 为顶点的三角形与
为顶点的三角形与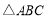 相似,求点
相似,求点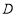 的坐标;
的坐标;
(3)如图2,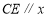 轴玮抛物线相交于点
轴玮抛物线相交于点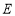 ,点
,点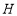 是直线
是直线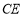 下方抛物线上的动点,过点
下方抛物线上的动点,过点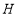 且与
且与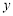 轴平行的直线与
轴平行的直线与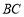 ,
,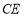 分别交于点
分别交于点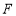 ,
,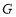 ,试探究当点
,试探究当点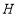 运动到何处时,四边形
运动到何处时,四边形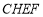 的面积最大,求点
的面积最大,求点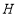 的坐标及最大面积;
的坐标及最大面积;
(4)若点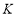 为抛物线的顶点,点
为抛物线的顶点,点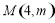 是该抛物线上的一点,在
是该抛物线上的一点,在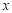 轴,
轴,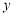 轴上分别找点
轴上分别找点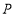 ,
,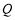 ,使四边形
,使四边形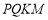 的周长最小,求出点
的周长最小,求出点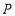 ,
,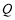 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com