练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

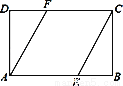
    已知：如图，在矩形ABCD中，点E，F分别在AB，CD边上，BE=DF，连接CE，AF．求证：AF=CE．

    证明见解析. 【解析】试题分析：根据矩形的性质得出 求出 根据平行四边形的判定得出四边形是平行四边形,即可得出答案. 试题解析： ∵四边形ABCD是矩形， ∴ ∴ ∴四边形是平行四边形，
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：安徽省亳州市涡阳县2017-2018学年度第一学期八年级期末联考数学试卷 题型：单选题

    有下列四个命题：①相等的角是对顶角；②同位角相等；③若一个角的两边与另一个角的两边互相平行，则这两个角一定相等；④从直线外一点到这条直线的垂线段，叫做点到直线的距离。其中是真命题的个数有（ ）

    A. 0个 B. 1个 C. 2个 D. 3个

    A 【解析】试题解析：①相等的角不一定是对顶角；是假命题； ②两直线平行，同位角相等．故原命题是假命题； ③若一个角的两边与另一个角的两边互相平行，则这两个角一定相等或互补，故原命题是假命题； ④从直线外一点到这条直线的垂线段的长度叫做这点到直线的距离；故原命题是假命题， 故选A．

    查看答案和解析>>

    科目：初中数学 来源：四川省遂宁市蓬溪县2017-2018学年七年级上学期期末考试数学试卷 题型：填空题

    下图（1）表示1张餐桌和6张椅子（每个小半圆代表1张椅子），若按这种方式摆放20张餐桌需要的椅子张数是 ．

    82． 【解析】试题分析：此类找规律的题目一定要结合图形进行分析，发现每多一张餐桌，就多4张椅子． 【解析】 结合图形发现：1张餐桌时，是6张椅子．在6的基础上，每多一张餐桌，就多4张椅子．则共有n张餐桌时，就有6+4（n﹣1）=4n+2．当n=20时，原式=4×20+2=82． 故答案为：82

    查看答案和解析>>

    科目：初中数学 来源：四川省遂宁市蓬溪县2017-2018学年七年级上学期期末考试数学试卷 题型：单选题

    数轴上到点-3的距离为3的点表示的数为 ( )

    A. 0 B. －6 C. －6或1 D. －6或0

    D 【解析】点在－3左侧时，与－3距离为3的点表示的数为－6；点在－3右侧时，与－3距离为3的点表示的数为3. 故选D.

    查看答案和解析>>

    科目：初中数学 来源：山东省济南市历城区2018届九年级上学期期末考试数学试卷 题型：解答题

    如图，一次函数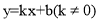的图象与反比例函数的图象交于二、四象限内的A、B两点，与x轴交于C点，点A的坐标为（- 3，4），点B的坐标为(6，n).

    （1）求该反比例函数和一次函数的解析式；

    （2）连接OB，求△AOB 的面积；

    （3）在x轴上是否存在点P，使△APC是直角三角形. 若存在，求出点P的坐标；若不存在，请说明理由．

    （1）反比例函数的解析式为y=﹣ ； 一次函数的解析式为y=﹣x+2； （2）；（3）存在，满足条件的P点坐标为（﹣3，0）、（﹣，0）． 【解析】试题分析：（1）先把代入得到的值，从而确定反比例函数的解析式为；再利用反比例函数解析式确定B点坐标为，然后运用待定系数法确定所求的一次函数的解析式为 即可求得. （3）过A点作轴于， 交x轴于，则点的坐标为；再证明利用相似比计算出则，所以...

    查看答案和解析>>

    科目：初中数学 来源：山东省济南市历城区2018届九年级上学期期末考试数学试卷 题型：填空题

    若，则__________．

    【解析】试题解析： 设 故答案为：

    查看答案和解析>>

    科目：初中数学 来源：山东省济南市历城区2018届九年级上学期期末考试数学试卷 题型：单选题

    如图，AB是⊙O的直径，直线DA与⊙O相切于点A，DO交⊙O于点C，连接BC，若∠ABC=21°，则∠ADC的度数为（　　）

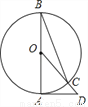
    A. 46° B. 47° C. 48° D. 49°

    C 【解析】【解析】 ∵OB=OC，∴∠B=∠BCO=21°，∴∠AOD=∠B+∠BCO=21°+21°=42°，∵AB是⊙O的直径，直线DA与⊙O相切与点A，∴∠OAD=90°，∴∠ADC=90°﹣∠AOD=90°﹣42°=48°．故选C．

    查看答案和解析>>

    科目：初中数学 来源：河北省唐山市路北区2017-2018学年度第一学期学生素质终期评价七年级数学试卷 题型：填空题

    已知2x+4与3x-2互为相反数,则x=______.

    【解析】试题解析：∵2x+4与3x-2互为相反数， ∴2x+4=-（3x-2）， 解得x=-． 故答案为：-．

    查看答案和解析>>

    科目：初中数学 来源：上海市虹口区2017学年九年级第一学期期终教学质量监控测试 题型：解答题

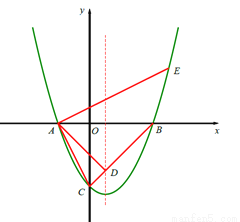
    如图，在平面直角坐标系xOy中，抛物线与x轴相交于点A（-2，0）、B（4，0），与y轴交于点C（0，-4），BC与抛物线的对称轴相交于点D．

    （1）求该抛物线的表达式，并直接写出点D的坐标；

    （2）过点A作AE⊥AC交抛物线于点E，求点E的坐标；

    （3）在（2）的条件下，点F在射线AE上，若△ADF∽△ABC，求点F 的坐标．

    （1），D（1，-3）；（2）；（3）或． 【解析】分析：（1）设抛物线的解析式为y=a(x+2)(x-4),将C（0，-4）代入求解即可；记抛物线的对称轴与x轴交点坐标为F，先求得抛物线的对称轴，则可得到FB的长，然后再证明△BFD为等腰直角三角形，从而可得到FD=FB=3，故此可得到点D的坐标；（2）过点E作EH⊥AB，垂为H．先证tan∠EAH=tan∠ACO=,设EH=t,则AH=2...

    查看答案和解析>>

    同步练习册答案