练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    下列运算正确的是（ ）

    A. B. C. D.

    D 【解析】试题解析：A. 故错误. B. 故错误. C. 故错误. D.正确. 故选D.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：贵州省铜仁市松桃县2018届九年级上学期第二次月考数学试卷 题型：解答题

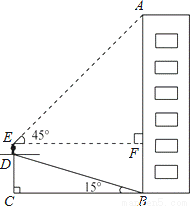
    小明为了测量楼房AB的高度，他从楼底的B处沿着斜坡向上行走20m，到达坡顶D处．已知斜坡的坡角为15°．（以下计算结果精确到0.1m）

    （1）求小明此时与地面的垂直距离CD的值；

    （2）小明的身高ED是1.6m，他站在坡顶看楼顶A处的仰角为45°，求楼房AB的高度．（sin15°≈0.2588，cos15°≈0.9659 ，tan≈.0.2677 )

    （1）小华与地面的垂直距离CD的值是5.2m； （2）楼房AB的高度是26.1m. 【解析】试题分析：（1）sin15°=，CD= BD·sin15°，将已知数值代入计算即可；（2）AB=AF+BF，BF=CD+ED不难求得，因为∠AEF=45°，所以AF=EF=BC，要求BC利用cos15°=，即BC=BD·cos15°. 试题解析： （1）在Rt△BCD中，∠CBD=15°，...

    查看答案和解析>>

    科目：初中数学 来源：山东省莒县第四协作区2017-2018学年度上学期第二次月考七年级数学试卷 题型：单选题

    将方程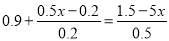变形正确的是（　　）

    A. 9+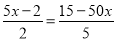 B. 0.9+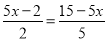

    C. 9+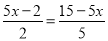 D. 0.9+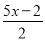=3﹣10x

    D 【解析】根据分数的性质：分母分子同时扩大10倍后分式的数值不变可得： 0.9+=3﹣10x 故选D.

    查看答案和解析>>

    科目：初中数学 来源：吉林省长春市2017-2018学年度 八年级数学期末测试卷 题型：填空题

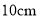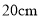    已知：等腰梯形的两底分别为和，一腰长为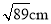，则它的对角线的长为______ .

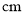    17 【解析】试题解析：如图，作DE⊥BC于E， ∵ABCD是等腰梯形,因而 在直角△CDE中，根据勾股定理得到DE=8， 在直角△BDE中,利用勾股定理得到 故答案为：17.

    查看答案和解析>>

    科目：初中数学 来源：吉林省长春市2017-2018学年度 八年级数学期末测试卷 题型：单选题

    如图：在菱形ABCD中，AC=6，BD=8，则菱形的边长为（ ）

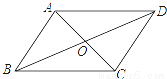
    A．5 B．10 C．6 D．8

    A 【解析】 试题分析：根据菱形的性质：菱形的对角线互相垂直平分，且每一条对角线平分一组对角，可知每个直角三角形的直角边，根据勾股定理可将菱形的边长求出． 【解析】 设AC与BD相交于点O， 由菱形的性质知：AC⊥BD，OA=AC=3，OB=BD=4 在Rt△OAB中，AB===5 所以菱形的边长为5． 故选：A．

    查看答案和解析>>

    科目：初中数学 来源：山东省临沂市2018届九年级（上）第一次月考数学试卷 题型：解答题

    将进价为40元的商品按50元的价格出售时，能卖出500个，已知该商品每涨价1元，其销售量就要减少10个，为了尽快减少库存，同时也为了赚取8000元的利润，售价应定为多少元？

    售价应定为60元． 【解析】试题分析：设涨价x元，则售价为（50+x）元，销售件，根据每件的盈利×销售的件数=赚取的利润，列方程求解即可． 试题解析：【解析】 设涨价x元，则售价为（50+x）元． 依题意列方程得（50+x﹣40）=8000． 整理得x2﹣40x+300=0， 解得x1=10，x2=30． 为了尽快减少库存，x=10， 50+10=60，...

    查看答案和解析>>

    科目：初中数学 来源：山东省临沂市2018届九年级（上）第一次月考数学试卷 题型：填空题

    若关于x的一元二次方程（m+3）x2+5x+m2+2m－3=0有一个根是0，则m= ，另一根为 。

    m=1 【解析】∵方程（m+3）x2+5x+m2+2m-3=0有一个根为0，∴将x=0代入方程得：m2+2m-3=0， 即（m-1）（m+3）=0，解得：m1=1，m2=-3，又原方程为关于x的一元二次方程，m+3≠0，即m≠-3，则m=1．那么方程为4x2+5x=0，解得x=0或∴另一个根是．

    查看答案和解析>>

    科目：初中数学 来源：天津市宝坻区口东镇2017-2018学年八年级12月月考数学试卷 题型：解答题

    计算下列各题：

    （1）（﹣2a）6﹣（﹣3a3）2+[﹣（2a）2]3

    （2）（16x4﹣8x3+4x2）÷（﹣2x）2

    （3）（2x﹣y）2﹣4（x﹣y）（x+2y）

    【答案】(1)﹣9a6；(2) 4x2﹣2x+1；(3)﹣8xy+9y2.

    【解析】试题分析：（1）利用积的乘方与幂的乘方运算法则计算后，合并即可得到结果； （2）利用多项式除以单项式的运算法则计算即可；（3）先利用乘法公式及多项式乘以多项式的运算法则计算后，再合并即可得结果.

    试题解析：

    (1)原式=64a6﹣9a6﹣64a6=﹣9a6；

    (2)原式=（16x4﹣8x3+4x2）÷4x2=4x2﹣2x+1；

    (3)原式=4x2﹣4xy+y2﹣4（x2﹣2xy﹣xy﹣2y2）=4x2﹣4xy+y2﹣4x2+8xy+4xy+8y2=﹣8xy+9y2.

    【题型】解答题
    【结束】
    22

    对下列多项进行因式分【解析】

    (1).（x+2）（x+4）+1.

    (2).x2﹣5x﹣6

    (3).（a2+4）2﹣16a2

    (4).18b（a﹣b）2﹣12（a﹣b）3

    (1)（x+3）2(2)（x﹣6）（x+1）；(3)（a+2）2（a﹣2）2；(4) 6（a﹣b）2（5b﹣2a） 【解析】试题分析：（1）先展开合并后利用完全平方公式因式分解即可；（2）利用十字相乘法因式分解即可；（3）先利用平方差公式，再利用完全平方公式分解因式即可；（4）直接利用提公因式法因式分解即可. 试题解析： (1)原式=x2+6x+9=（x+3）2. (2)原...

    查看答案和解析>>

    科目：初中数学 来源：浙江省金华市2017-2018学年七年级上册期末模拟数学试卷 题型：单选题

    下列计算正确的是（　　）

    A. x3+x2=x5 B. x3﹣x2=x C. x3÷x2=x D. x3•x2=x6

    C 【解析】A选项：x3与x2不是同类项，故是错误的； B选项：x3、－x2不是同类项，故是错误的； C选项：x3÷x2=x是正确的； D选项：x3•x2=x5,故是错误的. 故选C.

    查看答案和解析>>

    同步练习册答案