
��ͼ��ʾ����E����F��90�㣬��B����C��AE��AF�������½��ۣ���EM��FN����CD��DN���ۡ�FAN����EAM���ܡ�ACN�ա�ABM��������ȷ���У� ����
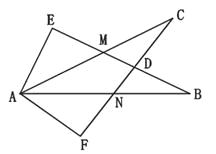
A. 1�� B. 2�� C. 3�� D. 4��
C �����������������������֪������������AAS�ж���AEB�ա�AFC�������ɸ���ȫ�������εó��Ľ������жϸ�ѡ���Ƿ���ȷ�� �ߡ�E=��F=90�㣬��B=��C��AE=AF�� ���AEB�ա�AFC����AAS�� ���FAM=��EAN�� ���EAN-��MAN=��FAM-��MAN������EAM=��FAN�����ʢ���ȷ�� �֡ߡ�E=��F=90�㣬AE=AF�� ���EAM... �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
��ͼ����E��F��BC�ϣ�BE=FC��AB=DC����B=��C����֤����A=��D��
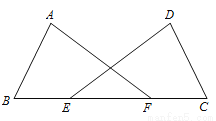
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018 ��ʦ������꼶��ѧ�²� �����¡�����֮��Ĺ�ϵ ��Ԫ���Ծ� ���ͣ������
��ͼ�ⳤΪa��С�����壬������ͼ�ķ��������ڷţ����϶��·ֱ�е�һ�㡢�ڶ��㡭��n�㣬��n���С������ĸ�����ΪS.����������⣺
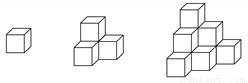
n | 1 | 2 | 3 | 4 | �� |
S | 1 | 3 | �� |
(1)��Ҫ����д�ϱ���
(2)�о��ϱ����Է���S��n�ı仯���仯����S��n�������������һ���Ĺ��ɣ�������ʽ������ʾS��n�Ĺ�ϵ�������㵱n��10ʱ��S��ֵΪ���٣�
(1)6,10(2)55 �������������������1������ͼ�ο�ֱ��ȷ����3��͵�4��С������ĸ������Ӷ���д���� ��2��������֪�������С������ĸ���Ϊ��1��ʼ��������Ȼ��֮�ͣ��ڵڼ���;ͼӵ��ڼ�����Ȼ��Ϊֹ���ݴ˿ɽ���n��С������ĸ�����ʾ����������������n=10�����ϲ��Ľ���м��㼴�ɵõ���Ӧ��S��ֵ. �����������1����ͼ��֪�����ϵ��£���һ����1��С�����壬�ڶ�����3��...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018 ��ʦ������꼶��ѧ�²� �����¡�����֮��Ĺ�ϵ ��Ԫ���Ծ� ���ͣ���ѡ��
ij��糡�����һ����Ϊ���Σ�����ϯ����λ�������з�ʽ���ã�
����(x) | 1 | 2 | 3 | 4 | �� |
���(y) | 50 | 53 | 56 | 59 | �� |
�����н��ۣ�������x���Ա�������λ��y���������������x�����������λ��y���Ա�������y��50��3x����y��47��3x��������ȷ�Ľ�����( )
A. 1�� B. 2�� C. 3�� D. 4��
B ������������ͼ����֪��������������,��λ��Ҳ����.��������x���Ա���,��λ��y��������� ����ͼ���е����ݿɵ�y=47+3x.�ʢ٢���ȷ. ��ѡ��B.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶��ѧ��4.3.2 �á��DZ߽ǡ��ǽDZߡ��ж�������ȫ�� ͬ����ϰ ���ͣ������
���ǰ������ڱ���ȵ��ı��ν��������Ρ� .��ͼ��ʾ�ı���ABCD��һ�����Σ�����AB��CB��AD��CD���Խ���AC��BD�ཻ�ڵ�O��OE��AB��OF��CB������ֱ���E��F.��֤��OE��OF.
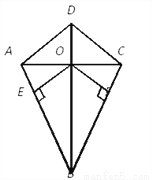
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶��ѧ��4.3.2 �á��DZ߽ǡ��ǽDZߡ��ж�������ȫ�� ͬ����ϰ ���ͣ���ѡ��
��ͼ��ʾ����֪��A����D����1����2����ôҪ�õ���ABC�ա�DEF����Ӧ�����������ǣ� ��
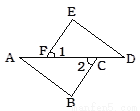
A. ��E����B B. ED��BC C. AB��EF D. AF��CD
D �����������⿼����ȫ�������ε��ж� �ж���ABC�ա�DEF�Ѿ��߱��������ǡ�A=��D����1=��2���ټ������ǵļб߶�Ӧ��ȣ��Ϳ�������ASA���ж�������ȫ�ȣ� ��AF=CD ��AC=DF �֡ߡ�A=��D����1=��2 ���ABC�ա�DEF ��ѡD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����ѧ���꼶�²������3.2�ù�ϵʽ��ʾ�ı������ϵ��ʱ��ϰ ���ͣ������
Ϊ�˽�ij��Ʒ��С�����ĺ����������Ƕ����ֳ��ڸ��ٹ�·�����˺������飬������������ݼ�¼�������Ƴ��±���
������ʻʱ��t��h�� | 0 | 1 | 2 | 3 | �� |
����ʣ������Q��L�� | 100 | 94 | 88 | 82 | �� |
�ٸ����ϱ������ݣ�����д��Q��t�Ĺ�ϵʽ��
��������ʻ5h�������е�ʣ�������Ƕ��٣�
�۸�Ʒ���������������50L������100km/h���ٶ�������ʻ���ó��������ʻ��Զ��
��Q=50��8t����������ʻ5h�������е�ʣ��������10L���۸ó��������ʻ625km. ��������������������ɱ����֪����ʼ�����е���Ϊ50L��ÿ��ʻ1Сʱ����������8L���ݴ˿ɵ�t��Q�Ĺ�ϵʽ�� ����������ʻ5h�������е�ʣ������������t=5ʱ��Q��ֵ�� ������50L���͵��������������������ʻ��Сʱ������Q=0ʱ��t��ֵ. ���������Q��t�Ĺ�ϵʽΪ��Q=50...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����ѧ���꼶�²������3.2�ù�ϵʽ��ʾ�ı������ϵ��ʱ��ϰ ���ͣ���ѡ��
ij��ǩ�ֱʵĵ���Ϊ2Ԫ����������ǩ�ֱ�x֧���ܼ�ΪyԪ����y��x֮��ĺ�����ϵʽΪ�� ��
A. y=-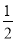 x B. y=
x B. y=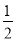 x C. y=-2x D. y=2x
x C. y=-2x D. y=2x
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶��ѧ��6.2.1 Ƶ�ʵ��ȶ��� ͬ����ϰ ���ͣ������
�о�����:һ�������ĺ���װ�����ɸ�ֻ����ɫ��һ���ĺ��������.�������㲻ͬ��ɫ�������?
��������:�ȴӺ�������8����,���ϼǺŷŻغ���,�ٽ�����������.���������Ҫ��:�Ƚ������,ÿ���������һ����,�Żغ���,�ټ���.
����:��������һ������50��,ͳ�ƽ�����±�:
�����ɫ | �Ǻ� | �мǺ� | ||
��ɫ | ��ɫ | ��ɫ | ��ɫ | |
�����Ĵ��� | 18 | 28 | 2 | 2 |
�Ʋ����.���������������������:
(1)���к������ռ�������İٷֱ��Ƕ���?
(2)�����к�����ٸ�?
 (1) ����Լռ40%,����Լռ60%��(2) 40��.
����������������1�����ݱ������ݿ��Եõ�50������ʵ���У����ֺ���20�Σ�����30�Σ��ɴ˼���������к������ռ�������İٷֱȣ���2���������֪50������ʵ���У������мǺŵ���4�Σ��ɴ˿��������������Ȼ�����ã�1���Ľ��ۼ���������к���
��������� (1)�������֪,50������������,���ֺ���20��,����30��,...
(1) ����Լռ40%,����Լռ60%��(2) 40��.
����������������1�����ݱ������ݿ��Եõ�50������ʵ���У����ֺ���20�Σ�����30�Σ��ɴ˼���������к������ռ�������İٷֱȣ���2���������֪50������ʵ���У������мǺŵ���4�Σ��ɴ˿��������������Ȼ�����ã�1���Ľ��ۼ���������к���
��������� (1)�������֪,50������������,���ֺ���20��,����30��,...�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com