练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

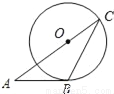
    如图，AB与⊙O相切于点B，AO的延长线交⊙O于点C，连结BC．若∠A=36°，则∠C=（　　）

    A. 54° B. 36° C. 27° D. 20°

    C 【解析】试题解析：如图，连接OB． ∵AB是⊙O切线， ∴OB⊥AB， ∴∠ABO=90°， ∵∠A=36°， ∴∠AOB=90°-∠A=54°， ∵OC=OB， ∴∠C=∠OBC， ∵∠AOB=∠C+∠OBC， ∴∠C=27°． 故选C．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：江苏省扬州市2016届九年级下学期二模数学试卷 题型：填空题

    埃是表示极小长度的单位名称，是为纪念瑞典物理学家埃基特朗而定的．1埃等于一亿分之一厘米，请用科学记数法表示1埃等于___________厘米．

    1×10-8 【解析】试题分析：此题考的是科学记数法： 由科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．因此1埃＝厘米.

    查看答案和解析>>

    科目：初中数学 来源：2017年海南省中考数学模拟试卷 题型：填空题

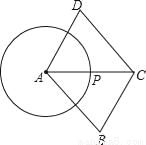
    如图，已知点P是半径为1的⊙A上一点，延长AP到C，使PC=AP，以AC为对角线作?ABCD．若AB=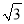，则?ABCD面积的最大值为_____．

    【解析】试题分析：由已知条件，根据平行四边形的性质和三角形的面积公式可知，要使ABCD的面积最大，只要△ABC的面积最大，即当AB、AC是直角边时所求面积最大.因此， 如答图，当AB⊥AC时， ∵AP=1，PC=AP，AB=， ∴.

    查看答案和解析>>

    科目：初中数学 来源：2017年海南省中考数学模拟试卷 题型：解答题

    已知关于x的方程kx2+（2k+1）x+2=0．

    （1）求证：无论k取任何实数时，方程总有实数根；

    （2）当抛物线y=kx2+（2k+1）x+2图象与x轴两个交点的横坐标均为整数，且k为正整数时，若P（a，y1），Q（1，y2）是此抛物线上的两点，且y1＞y2，请结合函数图象确定实数a的取值范围；

    （3）已知抛物线y=kx2+（2k+1）x+2恒过定点，求出定点坐标．

    （1）证明见解析；（2）a＞1或a＜﹣4；（3）抛物线恒过定点（0，2）、（﹣2，0）． 【解析】试题分析：（1）分类讨论：该方程是一元一次方程和一元二次方程两种情况．当该方程为一元二次方程时，根的判别式△≥0，方程总有实数根； （2）通过解kx2+（2k+1）x+2=0得到k=1，由此得到该抛物线解析式为y=x2+3x+2，结合图象回答问题． （3）根据题意得到kx2+（2k+...

    查看答案和解析>>

    科目：初中数学 来源：2017年海南省中考数学模拟试卷 题型：填空题

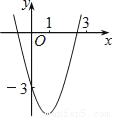
    如图，已知抛物线y=x2+bx+c经过点（0，﹣3），请你确定一个b的值，使该抛物线与x轴的一个交点在（1，0）和（3，0）之间．你确定的b的值是_____．

    1（在﹣2＜b＜2范围内的任何一个数） ． 【解析】试题分析：先把（0，-3）代入原函数y＝x 2＋bx＋c可得c=-3，所以函数变为y＝x 2＋bx-3，然后根据抛物线与x轴的一个交点在（1，0）和（3，0）之间，可知把（1，0）代入可得y=1+b-3＜0，解得b＜2；把（3，0）代入可得y=9+3b-3＞0，解得b＞-2；由此可知b的范围为：-2＜b＜2，因此只要是在这个范围的数都可以....

    查看答案和解析>>

    科目：初中数学 来源：2017年海南省中考数学模拟试卷 题型：单选题

    分式方程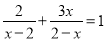的解为（　　）

    A. 1 B. 2 C. 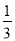D. 0

    A 【解析】试题分析：根据分式方程的解法：去分母，得2-3x=x-2，移项后解得x=1，检验x=1是原分式方程的根. 答案为A

    查看答案和解析>>

    科目：初中数学 来源：2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷（八） 题型：解答题

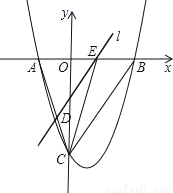
    如图，抛物线y=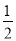x2﹣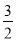x﹣9与x轴交于A、B两点，与y轴交于点C，连接BC、AC．

    （1）求AB和OC的长；

    （2）点E从点A出发，沿x轴向点B运动（点E与点A、B不重合），过点E作直线l平行BC，交AC于点D．设AE的长为m，△ADE的面积为s，求s关于m的函数关系式，并写出自变量m的取值范围；

    （3）在（2）的条件下，连接CE，求△CDE面积的最大值；此时，求出以点E为圆心，与BC相切的圆的面积（结果保留π）．

    （1）AB=9，OC=9；（2）s=m2（0＜m＜9）；（3）. 【解析】试题分析：（1）已知抛物线的解析式，当 可确定点坐标；当时，可确定点的坐标，进而确定的长． （2）直线 可得出相似，它们的面积比等于相似比的平方，由此得到关于的函数关系式；根据题干条件：点与点不重合，可确定的取值范围． （3）①首先用列出的面积表达式， 的面积差即为的面积，由此可得关于的函数关系式，根据函数的性质可...

    查看答案和解析>>

    科目：初中数学 来源：2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷（八） 题型：单选题

    如图⊙P经过点A（0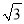， ）、O（0，0）、B（1，0），点C在第一象限的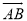上，则∠BCO的度数为（　　）

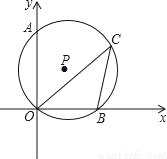
    A. 15° B. 30° C. 45° D. 60°

    B 【解析】试题解析：连接AB， ∵tan∠OAB=， ∴∠OAB=30°， ∴∠OCB=∠OAB=30°（圆周角定理）． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：黄金30题系列 八年级数学 大题好拿分 题型：解答题

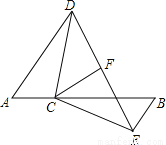
    如图，点C在线段AB上，AD∥EB，AC=BE，AD=BC，CF平分∠DCE．试探索CF与DE的位置关系，并说明理由．

    CF⊥DE，CF平分DE（三线合一）． 【解析】试题分析：根据平行线性质得出∠A=∠B，根据SAS证△ACD≌△BEC，推出DC=CE，根据等腰三角形的三线合一定理推出即可． 【解析】 CF⊥DE，CF平分DE，理由是： ∵AD∥BE， ∴∠A=∠B， 在△ACD和△BEC中 ， ∴△ACD≌△BEC（SAS）， ∴DC=CE， ∵CF平分∠...

    查看答案和解析>>

    同步练习册答案