
计算
(1)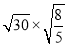 ;
;
(2)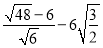 ;
;
(3) (1-cos30°)2+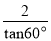 .
.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:湖南省2017-2018学年七年级数学上期末复习检测数学试卷 题型:解答题
若(2a+4)2+|4b﹣4|=0,求a+b的值?
﹣1 【解析】试题分析:根据非负数的性质列出方程求出a、b的值,代入所求代数式计算即可. 试题解析:由题意得,2a+4=0,4b﹣4=0, 解得,a=﹣2,b=1, 故a+b=﹣2+1=﹣1.查看答案和解析>>
科目:初中数学 来源:黑龙江省2017-2018学年七年级数学上学期期末试卷 题型:单选题
今年“地球停电一小时”活动的某地区烛光晚餐中,设座位有x排,每排坐30人,则有8人无座位;每排坐31人,则空26个座位.则下列方程正确的是( ) .
A. 30x-8=31x+26 B. 30x+8=31x+26
C. 30x-8=31x-26 D. 30x+8=31x-26
D 【解析】试题解析:设座位有x排,由题意得 30x+8=31x?26. 故选D.查看答案和解析>>
科目:初中数学 来源:宁夏2017-2018学年第一学期七年级上册数学期末试卷 题型:单选题
某中学开展“阳光体育活动”,九年级一班全体同学分别参加了巴山舞、乒乓球、篮球三个项目的活动,陈老师在此时统计了该班正在参加这三项活动的人数,并绘制了如图所示的频数直方图和扇形统计图.根据这两个统计图,可以知道此时该班正在参加乒乓球活动的人数是( )
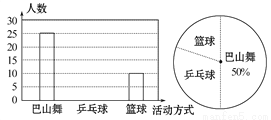
A. 50 B. 25 C. 15 D. 10
C 【解析】25÷50%=50(人),50-25-10=15(人),即参加乒乓球的活动人数为15.查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海南省海口市九年级数学科期末检测题 题型:解答题
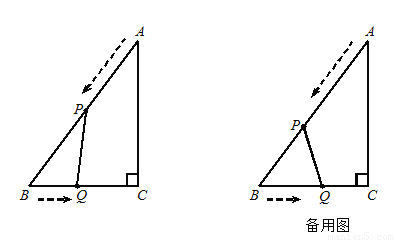
如图12,在△ABC中,∠C=90°,AB=10cm,BC=6cm. 点P从点A出发,沿AB边以2 cm/s的速度向点B匀速移动;点Q从点B出发,沿BC边以1 cm/s的速度向点C匀速移动. 当一个运动点到达终点时,另一个运动点也随之停止运动,设运动的时间为t(s).
(1)当PQ∥AC时,求t的值;
(2)当t为何值时,QB=QP;
(3)当t为何值时,△PBQ的面积等于4.8cm 2.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海南省海口市九年级数学科期末检测题 题型:单选题
如图,在△ABC中,AB=AC=5,BC=6,正方形DEFG的顶点D、G分别在AB、AC上,EF在BC上,则正方形DEFG的边长为( )
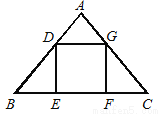
A. 2 B. 2.4 C. 2.5 D. 3
B 【解析】试题解析:过点作AM⊥BC于点M, ∵AB=AC=5,BC=6, 在Rt△ABM中, ∵四边形DEFG是矩形, ∴,DE⊥BC, ∴AN⊥DG,四边形EDMN是矩形, ∴MN=DE, 设MN=DE=x, ∵ ∴△ADG∽△ABC, ∴DG:BC=AN:AM, 解得: ∵四边形DEFG为正方形, ∴DE=...查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海南省海口市九年级数学科期末检测题 题型:单选题
关于x的一元二次方程x2+px-6=0的一个根为2,则p的值为( )
A. -2 B. 2 C. -1 D. 1
D 【解析】试题解析:把代入方程得 解得: 故选D.查看答案和解析>>
科目:初中数学 来源:宁夏2017-2018第一学年七年级上册数学期末综合检测模拟试卷 题型:填空题
如果x-2y=-3,那么5+x-2y=________.
2 【解析】∵x-2y=-3, ∴5+x-2y=5+(-3)=2.查看答案和解析>>
科目:初中数学 来源:山东省潍坊市诸城市2016-2017学年八年级(上)期末数学试卷 题型:解答题
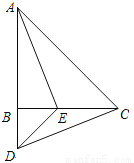
如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC.
① 求证:△ABE≌△CBD;
② 若∠CAE=30°,求∠BDC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com