练习册

  • 练习册
  • 试题
    相关习题
     0  17007  17015  17021  17025  17031  17033  17037  17043  17045  17051  17057  17061  17063  17067  17073  17075  17081  17085  17087  17091  17093  17097  17099  17101  17102  17103  17105  17106  17107  17109  17111  17115  17117  17121  17123  17127  17133  17135  17141  17145  17147  17151  17157  17163  17165  17171  17175  17177  17183  17187  17193  17201  366461 

    科目： 来源： 题型：解答题

    如图，是用硬纸板做成的两种直角三角形各有若干个，图①中两直角边长分别为a和b，斜边长为c；图②中两直角边长为c．请你动脑，将它们拼成一个能够证明勾股定理的图形．
    （1）请你画出一种图形，并验证勾股定理．
    （2）你非常聪明，能再拼出另外一种能证明勾股定理的图形吗？请画出拼后的图形（无需证明）．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    已知圆锥的底面半径是9cm，母线长为30cm，则其侧面展开图的圆心角是________度．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    已知关于x的方程mx2-（3m-1）x+2m-2=0
    （1）求证：无论m取任何实数时，方程恒有实数根；
    （2）若一元二次方程mx2-（3m-1）x+2m-2=0的两个实数根分别为x1，x2．且|x1-x2|=2，求m的值．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    计算：
    （1）数学公式；
    （2）数学公式．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    为了加强地方传统教育，实验中学举行了一次“知安阳、爱安阳知识竞赛”，共有900名学生参加了这次竞赛，为了解本次竞赛成绩，从中抽取了部分学生的成绩（得分取正整数，满分为100分）进行统计．请你根据下面尚未完成的频率分布表和频率分布直方图，解答下列问题：
    （1）填充频率颁表中的空格；
    （2）补全频率分布直方图；
    （3）全体参赛学生中，竞赛成绩落在哪组范围内的人数最多？
    （4）若成绩在90分以上（不含90分）为优秀，则该校成绩优秀的约为多少人？
    频率分布表：
    分组频数频率
    50.5～60.540.08
    60.5～70.580.16
    70.5～80.5100.20
    80.5～90.5160.32
    90.5～100.5
    合计

    查看答案和解析>>

    科目： 来源： 题型：解答题

    如图，已知平面直角坐标系，A、B两点的坐标分别为A（2，-3），B（4，-1）．
    （1）若P（p，0）是x轴上的一个动点，则当p=______时，△PAB的周长最短；
    （2）若C（a，0），D（a+3，0）是x轴上的两个动点，则当a=______时，四边形ABDC的周长最短；
    （3）设M，N分别为x轴和y轴上的动点，请问：是否存在这样的点M（m，0）、N（0，n），使四边形ABMN的周长最短？若存在，请求出m=______，n=______（不必写解答过程）；若不存在，请说明理由．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    如图，抛物线y=-数学公式x2+mx+n经过△ABC的三个顶点，点A坐标为（0，3），点B坐标为（2，3），点C在x轴的正半轴上．
    （1）求该抛物线的函数关系表达式及点C的坐标；
    （2）点E为线段OC上一动点，以OE为边在第一象限内作正方形OEFG，当正方形的顶点F恰好落在线段AC上时，求线段OE的长；
    （3）将（2）中的正方形OEFG沿OC向右平移，记平移中的正方形OEFG为正方形DEFG，当点E和点C重合时停止运动．设平移的距离为t，正方形DEFG的边EF与AC交于点M，DG所在的直线与AC交于点N，连接DM，是否存在这样的t，使△DMN是等腰三角形？若存在，求出t的值；若不存在，请说明理由；
    （4）在上述平移过程中，当正方形DEFG与△ABC的重叠部分为五边形时，请直接写出重叠部分的面积S与平移距离t的函数关系式及自变量t的取值范围；并求出当t为何值时，S有最大值，最大值是多少？

    查看答案和解析>>

    科目： 来源： 题型：填空题

    在平面直角坐标系中，A（2，-2），在y轴上确定点P，使△AOP为等腰三角形，则符合条件的P点共有________个，且P点坐标为________．

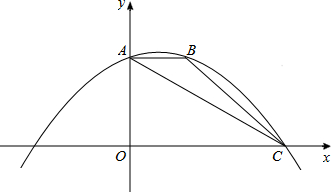
    查看答案和解析>>

    科目： 来源： 题型：解答题

    在“十一黄金周”期间，小明和他的父母坐游船从甲地到乙地观光，在售票大厅看到表（一），爸爸对小明说：“我来考考你，你能知道里程与票价之间有何关系吗？”小明点了点头说：“里程与票价是一次函数关系，具体是…”．
    在游船上，他注意到表（二），思考一下，对爸爸说：“若游船在静水中的速度不变，那么我还能算出它的速度和水流速度．”爸爸说：“你真聪明！”亲爱的同学，你知道小明是如何求出的吗？请你和小明一起求出：
    表（一）：
    出发时间到达时间
    甲→乙8：009：00
    乙→甲9：2010：00
    甲→乙10：2011：20
    ………
    表（二）
    里程（千米）票价（元）
    甲→乙1638
    甲→丙2046
    甲→丁1026
    ………
    （1）票价y（元）与里程x（千米）的函数关系式；
    （2）游船在静水中的速度和水流速度．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    已知在梯形ABCD中，AD∥BC，AD＜BC，且BC=6，AB=DC=4，点E是AB的中点，点P是BC边上一点．
    （1）当BP=2时．求证：△BEP∽△CPD；
    （2）若BP=5，过点P作射线PF，交CD所在的直线于点F，使得△BEP与△CPF相似．求此时CF的长度．

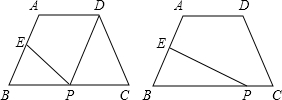
    查看答案和解析>>

    同步练习册答案