
科目: 来源:1+1轻巧夺冠·优化训练·八年级数学下 题型:044
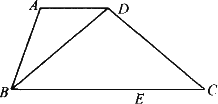
如图,在梯形ABCD中,AD∥BC,BD=CD,AB<CD,且∠ABC为锐角.若AD=4,BC=12,E为BC上一点.
问:当CE分别为何值时,四边形ABED是等腰梯形?直角梯形?请分别说明理由.
查看答案和解析>>
科目: 来源:1+1轻巧夺冠·优化训练·八年级数学下 题型:044
已知:如图,在直角梯形ABCD中,AD∥BC,BC=5 cm,CD=6 cm,∠DCB=60°,∠ABC=90°.等边三角形MPN(N为不动点)的边长为a cm,边MN和直角梯形ABCD的底边BC都在直线l上,NC=8 cm.将直角梯形ABCD向左翻折180°,翻折一次得到图形①,翻折两次得图形②,如此翻折下去.
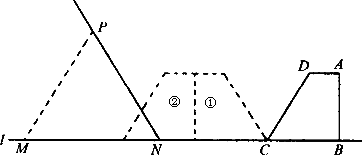
(1)将直角梯形ABCD向左翻折两次,如果此时等边三角形的边长a≥2 cm,则两图形重叠部分的面积是多少?
(2)将直角梯形ABCD向左翻折三次,如果第三次翻折得到的直角梯形与等边三角形重叠部分的面积等于直角梯形ABCD的面积,这时等边三角形的边长a至少应为多少?
(3)将直角梯形ABCD向左翻折三次,如果第三次翻折得到的直角梯形与等边三角形重叠部分的面积等于直角梯形面积的一半,这时等边三角形的边长应为多少?
查看答案和解析>>
科目: 来源:同步轻松练习 九年级数学下 题型:044
台风是一种自然灾害,它以台风中心为圆心在周围数十千米范围内形成气旋风暴,有极强的破坏力.据气象观测,距沿海某城市A的正南方向220 km的B处有一台风中心.其中心最大风力为12级,每远离台风中心20 km,风力就会减弱一级,该台风中心正以15 km/h的速度沿北偏东30°方向往C移动,且台风中心风力不变,如图所示.若城市所受风力达到或超过4级,则称为受台风影响.
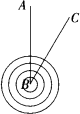
(1)该城市是否会受到这次台风的影响?请说明理由;
(2)若会受台风影响,那么台风影响该城市的持续时间有多长?
(3)该城市受到台风影响的最大风力为几级?
查看答案和解析>>
科目: 来源:同步轻松练习 九年级数学下 题型:044
如图,在一半径为168 cm的半圆形障碍物前600 cm处有一竖直的柱子.已知落在半圆上的影长为56π cm,同时,一直立70 cm杆子的影长为171 cm,求柱子的高度.(结果精确到1 cm.)

查看答案和解析>>
科目: 来源:同步轻松练习 九年级数学下 题型:044
如图,五一期间在某商贸大厦上从点A到点B悬挂了一条宣传条幅,小明和小雯的家正好住在商贸大厦对面的家属楼上.小明在四楼D点测得条幅端点A的仰角为30°,测得条幅端点B的俯角为45°;小雯在三楼C点测得条幅端点A的仰角为45°,测得条幅端点B的俯角为30°.若设楼层高度CD为3 m,请你根据小明和小雯测得的数据求出条幅AB的长.(参考数据:![]() ≈1.732,结果精确到1 m.)
≈1.732,结果精确到1 m.)

查看答案和解析>>
科目: 来源:同步轻松练习 九年级数学下 题型:044
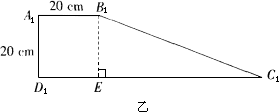
一段路基的横断面是直角梯形,如甲图所示,已知原来坡面的坡角α的正弦值为0.6,现不改变土石方量,全部利用原有土石方进行坡面改造,使坡度变小,达到如乙图所示的技术要求.试求出改造后坡面的坡度是多少?
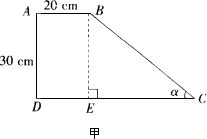
查看答案和解析>>
科目: 来源:同步轻松练习 九年级数学下 题型:044
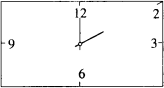
某课外学习小组在设计一个长方形时钟钟面时,欲使长方形的宽为20 cm,时钟的中心在长方形对角线的交点上,数字2在长方形的顶点上,数字3,6,9,12标在所在边的中点上,如图所示.
(1)问长方形的长应为多少?
(2)请你在长方框上点出数字1的位置,并说明确定该位置的方法;
(3)请你在长方框上点出钟面上其余数字的位置,并写出相应的数字(说明:要画出必要的、反映解题思路的辅助线).
查看答案和解析>>
科目: 来源:同步轻松练习 九年级数学下 题型:044
在△ABC中,∠A,∠B,∠C所对的边分别用a,b,c表示.
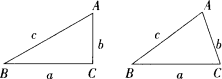
(1)如图,在△ABC中,∠A=2∠B,且∠A=60°.求证:a2=b(b+c);
(2)如果一个三角形的一个内角等于另一个内角的2倍,我们称这样的三角形为“倍角三角形”.本题第一问中的三角形是一个特殊的倍角三角形,那么对于任意的倍角三角形ABC,其中∠A=2∠B,关系式a2=b(b+c)是否仍然成立?请证明你的结论.
查看答案和解析>>
科目: 来源:同步轻松练习 九年级数学下 题型:044
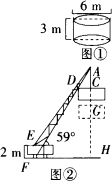
某种吊车的车身高EF=2 m,吊车臂AE=24 m,现要把如图①所示的圆柱形装饰物吊到14 m高的屋顶上安装.吊车在吊起的过程中,圆柱形的装饰物始终保持水平,如图②,若吊车臂与水平方向的夹角为59°,问能否吊装成功?(参考数据:sin59°≈0.8572,cos59°≈0.5150,tan59°≈1.6643.)
查看答案和解析>>
科目: 来源:同步轻松练习 九年级数学下 题型:044
如图,某海滨浴场的沿岸可以看作直线,1号救生员在岸边的A点看到海中的B点有人求救,便立即向前跑300 m到离B点最近的D点,再跳入海中游到B点救助;若每位救生员在岸上跑步的速度都是6 m/s,在水中游泳的速度都是2 m/s,∠BAD=45°.

(1)请问1号救生员的做法是否合理?
(2)若2号救生员从A跑到C,再跳入海中游到B点救助,且∠BCD=65°,请问谁先到达点B?(参考数据:sin65°≈0.9,cos65°≈0.4,tan65°≈2,![]() ≈1.4,结果精确到0.1 m.)
≈1.4,结果精确到0.1 m.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com