(2006湖北宜昌课改，22)如图，某一时刻太阳光从教室窗户射入室内，与地面的夹角∠BPC为30°，窗户的一部分在教室地面所形成的影长PE为3.5米，窗户的高度AF为2.5米．求窗外遮阳篷外端一点D到窗户上椽的距离AD．(结果精确0.1米)

(2006长春，20)如图，ABCD是供一辆机动车停放的车位示意图，请你参考图中数据，计算车位所占街道的宽度EF．

(参考数据：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84，结果精确到0.1m．)

(2006贵州课改，25)(10分)如图，某船以每小时36海里的速度向正东方向航行，在点A测得某岛C在北偏东60°方向上，航半小时后到达点B，测得该岛在北偏东30°方向上，已知该岛周围16海里内有暗礁．

(1)试说明点B是否在暗礁区域外？

(2)若继续向东航行有无触礁危险？请说明理由．

(2006，福州)我们知道，“直角三角形斜边上的高线将三角形分成两个与原三角形相似的直角三角形”，用这一方法，将矩形ABCD分割成大小不同的七个相似直角三角形，按从大到小的顺序编号为①至⑦(如图)，从而制成一副“三角七巧板”．

已知线段AB=1，∠BAC=θ．

(1)请用θ的三角函数表示线段BE的长：________；

(2)图中与线段BE相等的线段是________；

(3)仔细观察图形，求出⑦中最短的直角边DH的长(用θ的三角函数表示)．

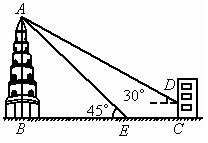
(2005　烟台)某风景区内有一古塔AB，在塔的北面有一建筑物，冬至日的正午光线与水平面的夹角是30°，此时塔在建筑物的墙上留下了高3m的影子CD；而在春分日正午光线与地面的夹角是45°，此时塔尖A在地面上的影子E与墙角C有15m的距离(B、E、C在一条直线上)，求塔AB的高度(结果保留根号，见图)

(2005　云南)九年级(3)班在完成测量校内旗杆高度的数学活动后，小明填写了如下《数学活动报告》中的附件(运算表)的一部分．请你根据此表提供的示意图及相关数据，完成此表未完成的部分：

(2005　北京)如图所示，河旁有一座小山，从山顶A处测得河对岸点C的俯角为30°，测得岸边点D的俯角为45°，又知河宽CD为50m，现需从山顶A到河对岸点C拉一条笔直的缆绳AC，求缆绳AC的长(答案可带根号)．

(2005　南京)如图所示，在两面墙之间有一个底端在A点的梯子，当它靠在一侧墙上时，梯子的顶端在B点；当它靠在另一侧墙上时，梯子的顶端在D点．已知∠BAC=60°，∠DAE=45°，点D到地面的垂直距离．求点B到地面的垂直距离BC．

(2005　江西)某课外学习小组在设计一个长方形时钟钟面时，欲使长方形的宽为20cm，时钟的中心在长方形对角线的交点上，数字2在长方形的顶点上，数字3、6、9、12标在所在边的中点上，如图所示．

(1)问长方形的长应为多少？

(2)请你在长方框上点出数字1的位置，并说明确定该位置的方法；

(3)请你在长方框上点出钟面上其余数字的位置，并写出相应的数字．(说明：要画必要的、反映解题思路的辅助线)

(2005　长春)如图所示，边长为1的正方形OABC的顶点A在x轴的正半轴上，将正方形OABC绕点O顺时针旋转30°，使点A落在抛物线(a＜0)的图像上．

(1)求抛物线的函数关系式；

(2)正方形OABC继续按顺时针旋转多少度时，点A再次落在抛物线的图像上？并求这个点的坐标．

(参考数据：．)