
科目: 来源:学习周报 数学 华师大八年级版 2009-2010学年 第18期 总第174期 华师大版 题型:044
一种电讯信号转发装置的发射直径为31 km.现要求在一边长为30 km的正方形城区选择若干个安装点,每个点安装一个这种转发装置,使这些装置转发的信号能完全覆盖这个城市.问:
(1)能否找到这样的4个安装点,使得这些点安装了这种转发装置后能达到预设的要求?
(2)至少需要选择多少个安装点,才能使这些点安装了这种转发装置后达到预设的要求?
答题要求:请在解答时,画出必要的示意图,并用必要的计算、推理和文字来说明你的理由.(图给出了几个边长为30 km的正方形城区示意图,供解题时选用)

查看答案和解析>>
科目: 来源:学习周报 数学 沪科九年级版 2009-2010学年 第19期 总第175期 沪科版 题型:044
一位小朋友在不打滑的平面轨道上滚动一个半径为
10 cm的圆盘,当滚动到与坡面BC开始相切时停止.其中AB=80 cm,BC与水平面的夹角为60°.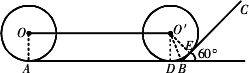
(1)求出圆盘在AB上滚动一圈时,其圆心所经过的路线的长度(π取3.14);
(2)当圆盘从点A滚动到与BC开始相切时停止,其圆心所经过的路线长大约是多少(精确到0.1 cm)?
查看答案和解析>>
科目: 来源:学习周报 数学 沪科九年级版 2009-2010学年 第17期 总第173期 沪科版 题型:044
如图,⊙
O是△ABC的外接圆,∠BAC与∠ABC的平分线相交于点I,延长AI交⊙O于点D,连接BD、DC.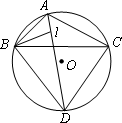
(1)求证:BD=DC=DI;
(2)若⊙O的半径为10 cm,∠BAC=120°,求△BDC的面积.
查看答案和解析>>
科目: 来源:学习周报 数学 沪科九年级版 2009-2010学年 第15期 总第171期 沪科版 题型:044
如图,已知
A、B、C、D是⊙O上的四个点,AB=BC,BD交AC于点E,连接CD、AD.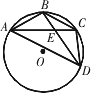
(1)求证:DB平分∠ADC;
(2)若BE=3,ED=6,求AB的长.
查看答案和解析>>
科目: 来源:学习周报 数学 沪科九年级版 2009-2010学年 第14期 总第170期 沪科版 题型:044
把两个全等的等腰直角三角板
ABC和EFG(其直角边长均为4)叠放在一起(如图a),且使三角板EFG的直角顶点G与三角板ABC斜边的中点O重合.现将三角板EFG绕点O顺时针旋转α(旋转角α满足条件:0°<α<90°),如图b,四边形CHGK是旋转过程中两个三角板的重叠部分.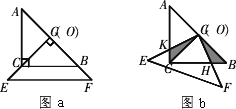
在上述旋转过程中,
BH与CK有怎样的数量关系?重叠部分的面积有何变化?请证明你的发现.查看答案和解析>>
科目: 来源:学习周报 数学 沪科九年级版 2009-2010学年 第13期 总第169期 沪科版 题型:044
已知某种水果的批发单价与批发量的函数关系如图所示.
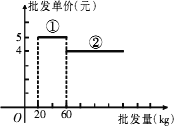
(1)请说明上图中①、②两段函数图象的实际意义;
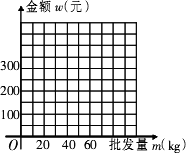
(2)写出批发该种水果的资金金额w(元)与批发量m(kg)之间的函数关系式;在下图的坐标系中画出该函数图象;指出金额在什么范围内,以同样的资金可以批发到较多数量的该种水果;
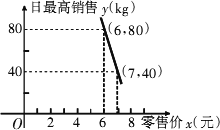
(3)经调查,某经销商销售该种水果的日最高销量y与零售价x之间的函数关系如图所示,该经销商拟每日售出60 kg以上该种水果,且当日零售价不变,请你帮助该经销商设计进货和销售的方案,使得当日获得的利润W最大.
查看答案和解析>>
科目: 来源:学习周报 数学 沪科九年级版 2009-2010学年 第13期 总第169期 沪科版 题型:044
如下图,有一个呈直角三角形的不锈钢片,已知∠
C=90°,AB=5 cm,BC=3 cm.试设计一种方案,用这个不锈钢片裁出一个面积最大的正方形,并求出它的面积.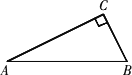
查看答案和解析>>
科目: 来源:学习周报 数学 沪科九年级版 2009-2010学年 第12期 总第168期 沪科版 题型:044
如图,足球场上守门员从点
O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距点O6米的B处发现球在自己头的正上方达到最高点M,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.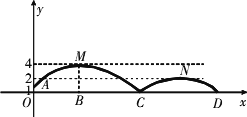
(1)求足球开始飞出到第一次落地时,该抛物线的函数关系式;
(2)足球第一次落地点C距守门员约多少米(取4![]() ≈7)?
≈7)?
(3)运动员乙要抢到第二个落地点D,他应再向前跑多少米(取2![]() ≈5)?
≈5)?
查看答案和解析>>
科目: 来源:学习周报 数学 沪科九年级版 2009-2010学年 第12期 总第168期 沪科版 题型:044
善于不断改进学习方法的小虎发现,对解题进行回顾反思,学习效果会更好.某一天小虎有
20分钟时间可用于学习.假设小虎解题的学习收益量y1与用于解题的时间x1(单位:分钟)的关系如图1所示,回顾反思的学习收益量y2与用于回顾反思的时间x2(单位:分钟)的关系如图2所示(其中OA是抛物线的一部分,A为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.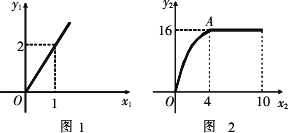
(1)求小虎解题的学习收益量y1与用于解题的时间x1之间的函数关系式;
(2)求小虎回顾反思的学习收益量y2与用于回顾反思的时间x2的函数关系式;
(3)问小虎如何分配解题和回顾反思的时间,才能使这20分钟的学习收益总量最大?最大值为多少?
查看答案和解析>>
科目: 来源:学习周报 数学 沪科九年级版 2009-2010学年 第12期 总第168期 沪科版 题型:044
如图,某公路隧道横截面为抛物线,其最大高度为
6米,底部宽度OM为12米.现以点O为原点,OM所在直线为x轴建立直角坐标系.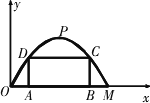
(1)直接写出点M及抛物线的顶点P的坐标;
(2)求这条抛物线的函数关系式;
(3)若要搭建一个矩形“支撑架”AD-DC-CB,使C、D两点在抛物线上,A、B两点在地面OM上,则这个“支撑架”总长的最大值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com