如图是某货站传送货物的平面示意图．为了提高传送过程的安全性，工人师傅欲减小传送带与地面的夹角，使其由45°改为3°．已知原传送带AB长为4米．

(1)求新传送带AC的长度；

(2)如果需要在货物着地点C的左侧留出2米的通道，试判断距离B点4米的货物MNQP是否需要挪走，并说明理由．(说明：(1)(2)的计算结果精确到0.1米，参考数据：≈1.41，≈1.73，≈2.24，≈2.45)

在图1至图2中，点B是线段AC的中点，点D是线段CE的中点．四边形BCGF和CDHN都是正方形．AE的中点是M．

(1)如图1，点E在AC的延长线上，点N与点G重合时，点M与点C重合，求证：FM＝MH，FM⊥MH；

(2)将图1中的CE绕点C顺时针旋转一个锐角，得到图2，求证：△FMH是等腰直角三角形；

已知在△ABC中，∠A＝45°，AB＝7，tanB＝，动点P、D分别在射线AB、AC上，且∠DPA＝∠ACB，设AP＝x，△PCD的面积为y．

(1)求△ABC的面积；

(2)如图，当动点P、D分别在边AB、AC上时，求y关于x的函数解析式，并写出函数的定义域；

(3)如果△PCD是以PD为腰的等腰三角形，求线段AP的长．

如图，已知二次函数y＝x²＋bx＋c的图像经过点A(4，0)和点B(3，－2)，点C是函数图像与y轴的公共点．过点C作直线CE∥AB．

(1)求这个二次函数的解析式；

(2)求直线CE的表达式；

(3)如果点D在直线CE上，且四边形ABCD是等腰梯形，求点D的坐标．

如图，点M(4，0)，以点M为圆心、2为半径的圆与x轴交于点A、B．已知抛物线过点A和B，与y轴交于点C．

(1)求点C的坐标，并画出抛物线的大致图象．

(2)求出抛物线的顶点D的坐标，并确定与圆M的位置关系．

(3)点Q(8，m)在抛物线上，点P为此抛物线对称轴上一个动点，求PQ＋PB的最小值．

如图，抛物线y＝ax²＋bx＋c的对称轴为直线x＝1，与x轴交于A、B两点，与y轴交于点C，其中A(－1，0)、C(0，3)．

(1)求此抛物线的解析式；

(2)若此抛物线的顶点为P，将△BOC绕着它的顶点B顺时针在第一象限内旋转，旋转的角度为α，旋转后的图形为△B．

①当∥CP时，求α的大小；

②△BOC在第一象限内旋转的过程中，当旋转后的△B有一边与BP重合时，求△B不在BP上的顶点的坐标．

为了参观上海世博会，某公司安排甲、乙两车分别从相距300千米的上海、泰州两地同时出发相向而行，甲到泰州带客后立即返回，下图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象．

(1)请直接写出甲离出发地的距离y(千米)与行驶时间x(小时)之间的函数关系式，并写出自变量x的取值范围；

(2)当它们行驶4.5小时后离各自出发点的距离相等，求乙车离出发地的距离y(千米)与行驶时间x(小时)之间的函数关系式，并写出自变量x的取值范围；

(3)在(2)的条件下，甲、乙两车从各自出发地驶出后经过多少时间相遇？

如图，在平面直角坐标系中，已知点B(2，0)、A(m，0)(0＜m＜)，以AB为边在x轴下方作正方形ABCD，点E是线段OD与正方形ABCD的外接圆的交点，连接BE与AD相交于点F．

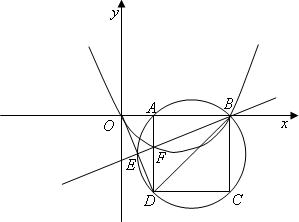
(1)求证：BF＝DO；

(2)若，试求经过B、F、O三点的抛物线l的解析式；

(3)在(2)的条件下，将抛物线l在x轴下方的部分沿x轴翻折，图像的其余部分保持不变，得到一个新图像，若直线BE向上平移t个单位与新图像有两个公共点，试求t的取值范围．

2010年5月1日，第41届世界博览会在上海市举行，本次世博会的主题是“城市，让生活更美好”(Better City, Better Life)．主办机构预计吸引世界各地7000万人次参观者前往，总投资达450亿人民币，是世界博览会史上最大规模．世博园某馆前有一块边长为8米的正方形花圃，如图AE＝AF，点G、H、I分别是EF、CE、CF的中点，计划在△GHI内放置吉祥物“海宝”塑像，在阴影部分种植江苏荷花，其余部分种植广西茉莉．原来种植1平方米荷花和1平方米茉莉的总成本为200元，受季节和气候的影响，经核算荷花的种植成本提高了2成，茉莉的种植成本降低了1成，使每平方米荷花和每平方米茉莉的种植总成本提高了8％．

(1)试求出实际1平方米荷花和1平方米茉莉种植成本分别是多少元？

(2)若此花圃实际种植总成本为7956元，请求出AE的长度．