如图，点D，E分别在△ABC的边BC，BA上，四边形CDEF是等腰梯形，EF∥CD．EF与AC交于点G，且∠BDE∠A．

(1)试问：AB·FG＝CF·CA成立吗？说明理由；

(2)若BD＝FC，求证：△ABC是等腰三角形．

如图，PA为⊙O切线，A为切点，PBC为割线，∠APC的平分线交AB于点E，交AC于点F，点M为的中点．

求证：AM⊥PF

如下图，在△ABC中，∠ACB＝90°，D是AB的中点，以DC为直径的⊙O交△ABC的边于G，F，E点．

求证：(1)F是BC的中点；

(2)∠A＝∠GEF．

阅读下面问题的解决过程：

问题解决：

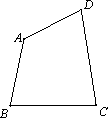
如图，已知四边形ABCD，过点B作一直线(不必写作法)，使其等分四边形ABCD的面积，并证明．

如图，已知AB是⊙O的直径，点C在⊙O上，P是△OAC的重心，且，∠A＝30°．

(1)求劣弧的长；

(2)若∠ABD＝120°，BD＝1，求证：CD是⊙O的切线．

如图，AB，BC分别是⊙O的直径和弦，点D为上一点，弦DE交⊙O于点E，交AB于点F，交BC于点G，过点C的切线交ED的延长线于H，且HC＝HG，连接BH，交⊙O于点M，连接MD，ME．

求证：(1)DE⊥AB；

(2)∠HMD＝∠MHE＋∠MEH．

如图1，线段PB过圆心O，交圆O于A，B两点，PC切圆O于点C，作AD⊥PC，垂足为D，连结AC，BC．

(1)写出图1中所有相等的角(直角除外)，并给出证明；

(2)若图1中的切线PC变为图2中割线PCE的情形，PCE与圆O交于C，E两点，AE与BC交于点M，AD⊥PE，写出图2中相等的角(写出三组即可，直角除外)；

(3)在图2中，证明：AD·AB＝AC·AE．

如图，在△ABC和△DEF中，∠A＝∠D＝90°，AB＝DE＝3，AC＝2DF＝4．

(1)判断这两个三角形是否相似？并说明为什么？

(2)能否分别过A，D在这两个三角形中各作一条辅助线，使△ABC分割成的两个三角形与△DEF分割成的两个三角形分别对应相似？证明你的结论．