
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
 相同的高度飞行3千米到B处,此时观测目标C的俯角是60°,求此山的高度CD.(精确到0.1)
相同的高度飞行3千米到B处,此时观测目标C的俯角是60°,求此山的高度CD.(精确到0.1) ,
, )
)查看答案和解析>>
科目: 来源: 题型:填空题
 如图,EF∥AD,∠1=∠2.说明:∠DGA+∠BAC=180°.请将说明过程填写完成.
如图,EF∥AD,∠1=∠2.说明:∠DGA+∠BAC=180°.请将说明过程填写完成.查看答案和解析>>
科目: 来源: 题型:解答题
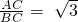 ,则∠B=60°;现在已知关于x的一次函
,则∠B=60°;现在已知关于x的一次函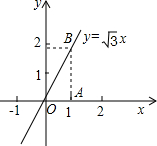 数
数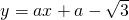 .
.查看答案和解析>>
科目: 来源: 题型:解答题
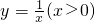 的图象交于点P,以P为圆心,2倍OP的长为半径作弧,在∠AOB内部交函数
的图象交于点P,以P为圆心,2倍OP的长为半径作弧,在∠AOB内部交函数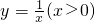 的图象于点R;
的图象于点R; ∠AOB.
∠AOB.
 ,求直线OM对应的函数表达式(用含a,b的代数式表示);
,求直线OM对应的函数表达式(用含a,b的代数式表示); ∠AOB;
∠AOB;查看答案和解析>>
科目: 来源: 题型:解答题
 近年来,“宝胜”集团根据市场变化情况,采用灵活多样的营销策略,产值、利税逐年大幅度增长.第六销售公司2004年销售某型号电缆线达数万米,这得益于他们较好地把握了电缆售价与销售数量之间的关系.经市场调研,他们发现:这种电缆线一天的销量y(米)与售价x(元/米)之间存在着如图所示的一次函数关系,且40≤x≤70.
近年来,“宝胜”集团根据市场变化情况,采用灵活多样的营销策略,产值、利税逐年大幅度增长.第六销售公司2004年销售某型号电缆线达数万米,这得益于他们较好地把握了电缆售价与销售数量之间的关系.经市场调研,他们发现:这种电缆线一天的销量y(米)与售价x(元/米)之间存在着如图所示的一次函数关系,且40≤x≤70.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com