科目： 来源： 题型：选择题

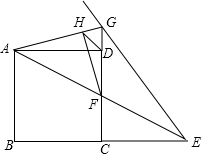4．如图，点E是正方形ABCD的边BC延长线一点，连接AE交CD于F，作∠AEG=∠AEB，EG交CD的延长线于G，连接AG，当CE=BC=2时，作FH⊥AG于H，连接DH，则DH的长为（　　）

A．

2-$\sqrt{2}$

B．

$\sqrt{2}-1$

C．

$\frac{\sqrt{2}}{2}$

D．

$\frac{2}{3}$

科目： 来源： 题型：解答题

3．如图，点P是等腰Rt△ABC底边BC上一点，过点P作BA、AC的垂线，垂足为E、F，设点D为BC中点，求证：△DEF是等腰直角三角形．

科目： 来源： 题型：解答题

2．如图，在平面直角坐标系中，⊙O交x轴于A、B两点，点P为圆上一动点PQ⊥x轴于点Q，点P运动到某一时刻：PQ=$\sqrt{3}$，AQ=3．
（1）求⊙O的半径；
（2）当点C（m，n）在第三象限的圆弧上运动，CD⊥x轴于D，在x轴上取一点I（点I在点D的左侧），使ID=CD，过点I作x 轴的垂线，并在垂线上取一点T（点T在x轴上方），将TC绕点T逆时针旋转90°得到线段TM，MN⊥x轴于点N，设IT=p，MN=q，判断关于x的方程：nx²+qx-p=0根的情况；
（3）在（2）的条件下，作直线MI，判断当点P运动过程中，直线MI与⊙O的位置关系，并判断m的取值情况．

科目： 来源： 题型：填空题

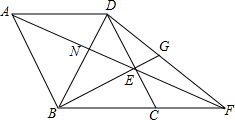1．如图，在菱形ABCD中，∠ABC=120°，点E在边CD上（DE＞CE），连结AE并延长交BC的延长线于点F，连结DF，连结BE并延长交DF于点G．若BE：EG=49：15，CF=6，则线段DN的长为$\frac{50}{13}$．

科目： 来源： 题型：解答题

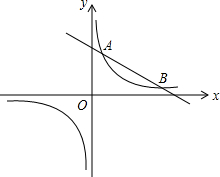20．如图，双曲线y=$\frac{k}{x}$（k＞0）与直线y=-$\frac{1}{2}$x+4相交于A，B两点．
（1）当k=6时，求点A，B的坐标；
（2）在双曲线y=$\frac{k}{x}$（k＞0）的同一支上有三点M（x₁，y₁），N（x₂，y₂），P（$\frac{{x}_{1}+{x}_{2}}{2}$，y₀），请你借助图象，直接写出y₀与$\frac{{y}_{1}+{y}_{2}}{2}$的大小关系．

科目： 来源： 题型：填空题

科目： 来源： 题型：解答题

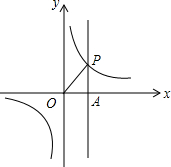18．如图，函数y=$\frac{k}{x}$的图象与直线x=2交于第一象限的点P，△AOP的面积等于$\frac{1}{2}$．
（1）利用图象，求当0＜x＜2时，y的取值范围；
（2）设P₁（x₁，y₁），P₂（x₂，y₂）是函数y=$\frac{k}{x}$图象上的任意不重合的两点，M=$\frac{{y}_{1}}{{x}_{1}}$+$\frac{{y}_{2}}{{x}_{2}}$，N=$\frac{{y}_{2}}{{x}_{1}}$+$\frac{{y}_{1}}{{x}_{2}}$试判断M，N的大小．并说明理由．

科目： 来源： 题型：解答题

科目： 来源： 题型：解答题

16．如图，已知一条直线经过点A（0，2）、点B（1，0），将这条直线向左平移与x轴、y轴分别交与点C、点D，
（1）求直线AB的函数解忻式；
（2）计算OD-2BC的值．

科目： 来源： 题型：解答题

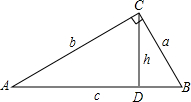15．小叶从计算中得到这样的结论：如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D．设BC=a，AC=b，AB=c，CD=h，则有等式$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=$\frac{1}{{h}^{2}}$成立．请你判断小叶的结论是否正确？若正确，请给予证明；若不正确，请说明理由．