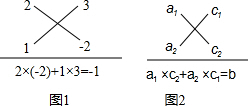5．【知识经验】
我们已经学过将一个多项式分解因式的方法有提公因式法和运用公式法，其实分解因式的方法还有很多，下面我们一起再学习三种因式分解的方法吧．
【学习拓展】
（1）分组分解法：将-个多项式适当分组后，可提公因式或运用公式继续分解因式的方法．
例x²-2xy+y²+4x-4y=（x²-2xy+y²）+（4x-4y）=（x-y）（x-y+4）．
分组分解法中分组的目的是：分组后小组内及小组之间能提公因式或运用公式．
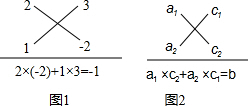
（2）十字相乘法
例 分解因式：2x²-x-6．
分析：二次项系数2分解成2与1的积；常数项-6分解成-l与6（或-6与1，
-2与3，-3与2）的积，但只有当-2与3按如图1所示方式排列，然后交叉相乘的和正好等于一次项系数-l．
所以：2x²-x-6=-（2x+3）（x-2）．
小结：用十字相乘法分解形如ax²+bx+c时，二次项系数a分解成    a₁与a₂的积，分别写在十字交叉线的左上角和左下角；常数项c    分解成c₁与c₂的积，分别写在十字交叉线的右上角和右下角，把a_l，a₂，c_l，c₂按如图2所示方式排列，当且仅当a_lc₂+a₂c_l=6（一次项系数）时，ax²+bx+c可分解因式．即ax²+bx+c=（a_lx+c₁）（a₂x+c₂）．
（3）拆项法：将一个多项式的某一项拆成两项后，重新分组，可提公因式或运用公式继续分解的方法．
例 3x³+7x²-4
=3x³-2x²+9x2-4（拆项）
=（3x³-2x²）+（9x²-4）（分组分解）
=x²（3x-2）+（3x+2）（3x-2）
=（3x-2）（x²+3x+2）（十字相乘法）
=（3x-2）（x+1）（x+2）（达到每一个多项式因式不能再分解为止）
【学以致用】利用上面的方法将下列各式分解因式：
（1）a³+2a²+4a+8；    （2）3x²+2x-5；    （3）x³+3x²-4．

4．如图，平面镜A与B之间夹角（∠AOB）为150°，光线经过平面镜A反射后射在平面镜B上，再反射出去．若∠1=∠2，则∠1=15度．

3．因式分解：-3x²+27=-3（x+3）（x-3）．

2．若多项式x²+ax+b分解因式的结果（x-2）（x+3），则a，b的值分别是（　　）

A．

a=1，b=-6

B．

a=5，b=6

C．

a=1，b=6

D．

a=5，b=-6

1．计算：103²-97²=1200．

20．方程ax-2y=5的一个解是$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$，则a的取值是（　　）

A．

9

B．

-9

C．

1

D．

-1

19．计算：1²-2²+3²-4²+5²-6²+7²-8²+…-78²+79²=3160．

18．已知∠AOB=50°，∠BOD=30°，则∠AOD=20°或80°．

17．观察下列各式：
$\sqrt{1+\frac{1}{{1}^{2}}+\frac{1}{{2}^{2}}}$=1+$\frac{1}{1}$-$\frac{1}{2}$=1$\frac{1}{2}$；$\sqrt{1+\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}}$=1+$\frac{1}{2}$-$\frac{1}{3}$=1$\frac{1}{6}$；
$\sqrt{1+\frac{1}{{3}^{2}}+\frac{1}{{4}^{2}}}$=1+$\frac{1}{3}$-$\frac{1}{4}$=1$\frac{1}{12}$，…
请你根据以上三个等式提供的信息解答下列问题
①猜想：$\sqrt{1+\frac{1}{{7}^{2}}+\frac{1}{{8}^{2}}}$=1+$\frac{1}{7}$-$\frac{1}{8}$=1$\frac{1}{56}$；
②归纳：根据你的观察，猜想，请写出一个用n（n为正整数）表示的等式：$\sqrt{1+\frac{1}{{n}^{2}}+\frac{1}{（n+1）^{2}}}$=1+$\frac{1}{n}$-$\frac{1}{n+1}$=$\frac{{n}^{2}+n+1}{{n}^{2}+n}$；
③应用：计算$\sqrt{\frac{82}{81}+\frac{1}{100}}$．

16．解方程：$\frac{2}{3}$x=$\frac{1}{12}$x²+$\frac{3}{x^2}$+$\frac{4}{x}$．