（1）解方程：2x2+3=7x；　 （2）解方程：（2x+1）2+4（2x+1）+3=0．

已知抛物线y=a（x﹣3）2+2经过点（1，﹣2）．

（1）求a的值；

（2）若点A（m，y1）、B（n，y2）（m＜n＜3）都在该抛物线上，试比较y1与y2的大小．

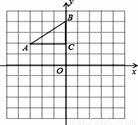
如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是，B（0，4），C（0，2）．

（1）将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△A1B1C；平移△ABC，若点A对应点A2的坐标为（0，），画出平移后对应的△A2B2C2；

（2）若将△A1B1C绕某一点旋转可以得到△A2B2C2；请直接写出旋转中心的坐标；

（3）在x轴上有一点P，使得PA+PB的值最小，请直接写出点P的坐标．

已知二次函数y=x2﹣x﹣6．

（1）画出函数的图象；

（2）观察图象，指出方程x2﹣x﹣6=0的解及不等式x2﹣x﹣6＞0解集；

（3）求二次函数的图象与坐标轴的交点所构成的三角形的面积．

如图，已知：点O是∠EPF的平分线上的一点，以点O为圆心的圆与角的两边分别交于点A、B和C、D。

（1）求证： =；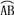

（2）若角的顶点P在圆内，上述结论还成立吗？若不成立，请说明理由；若成立，请加以证明。

已知，关于的一元二次方程有两个不相等的实数根，

（1）求K的取值范围 ；

（2）如两根为x1,x2，且满足，求K的值.

小明设计了点做圆周运动的一个动画游戏，如上图所示，甲、乙两点分别从直径的两端点A、B以顺时针、逆时针的方向同时沿圆周运动，甲运动的路程l（cm）与时间t（s）满足关系：l=t2+t（t≥0），乙以4cm/s的速度匀速运动，半圆的长度为21cm．

（1）甲运动4s后的路程是多少？

（2）甲、乙从开始运动到第一次相遇时，它们运动了多少时间？

（3）甲、乙从开始运动到第二次相遇时，它们运动了多少时间？

淘宝网上某店铺经营某种型号的童装．根据第一周的销售记录，该型号服装每天的售价（元/件）与当日的销售量（件）的相关数据如下表：

已知该型号童装每件的进价是70元，同时为吸引顾客，该店铺承诺，每件服装的快递费10元由卖家承担．

（1）请观察题中的表格，用所学过的一次函数、反比例函数或二次函数的有关知识，求第一周销售中，与的函数关系式；

（2）设第一周每天的赢利为元，求关于的函数关系式，并求出每天的售价为多少元时，每天的赢利最大？最大赢利是多少？

ABCD中，E是CD边上一点，

（1）将△ADE绕点A按顺时针方向旋转，使AD、AB重合，得到△ABF，如图1所示．观察可知：与DE相等的线段是　 　，∠AFB=∠　 　

（2）如图2，正方形ABCD中，P、Q分别是BC、CD边上的点，且∠PAQ=45°，试通过旋转的方式说明：DQ+BP=PQ；

（3）在（2）题中，连接BD分别交AP、AQ于M、N，你还能用旋转的思想说明BM2+DN2=MN2吗？

（11分）如图，边长为8的正方形OABC的两边在坐标轴上，以点C为顶点的抛物线经过点A，点P是抛物线上点A、C间的一个动点（含端点），过点P作PF⊥BC于点F. 点D、E的坐标分别为（0，6），（-4，0），连接PD，PE，DE.

（1）请直接写出抛物线的解析式；

（2）小明探究点P的位置发现：当点P与点A或点C重合时，PD与PF的差为定值. 进而猜想：对于任意一点P，PD与PF的差为定值. 请你判断该猜想是否正确，并说明理由；

（3）小明进一步探究得出结论：若将“使△PDE的面积为整数”的点P记作“好点”，则存在多个“好点”，且使△PDE的周长最小的点P也是一个“好点”.请直接写出所有“好点”的个数，并求出△PDE的周长最小时“好点”的坐标.