
科目: 来源:2018届人教版九年级数学下册同步专题练习:专项训练七 相似 题型:填空题
如图,直线l1、l2、…l6是一组等距的平行线,过直线l1上的点A作两条射线,分别与直线l3、l6相交于点B、E、C、F.若BC=2,则EF的长是 5 .

查看答案和解析>>
科目: 来源:2018届人教版九年级数学下册同步专题练习:专项训练七 相似 题型:填空题
已知:在平行四边形ABCD中,点E在直线AD上,AE= AD,连接CE交BD于点F,则EF:FC的值是__.
AD,连接CE交BD于点F,则EF:FC的值是__.
查看答案和解析>>
科目: 来源:2018届人教版九年级数学下册同步专题练习:专项训练七 相似 题型:解答题
如图,在8×8的正方形网格中,△CAB和△DEF的顶点都在边长为1的小正方形的顶点上.
(1)填空:AC=________,AB=________;
(2)判断△CAB和△DEF是否相似,并说明理由.

查看答案和解析>>
科目: 来源:2018届人教版九年级数学下册同步专题练习:专项训练七 相似 题型:填空题
如图,要在宽为22米的滨湖大道AB两边安装路灯,路灯的灯臂CD长为2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的中轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳。此时,路灯的灯柱BC高度应该设计为 .

查看答案和解析>>
科目: 来源:2018届人教版九年级数学下册同步专题练习:专项训练七 相似 题型:解答题
如图,⊙O的半径为5,点P在⊙O外,PB交⊙O于A、B两点,PC交⊙O于D、C两点.
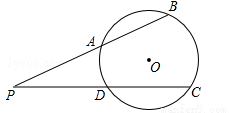
(1)求证:PA•PB=PD•PC;
(2)若PA=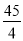 ,AB=
,AB=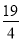 ,PD=DC+2,求点O到PC的距离.
,PD=DC+2,求点O到PC的距离.
查看答案和解析>>
科目: 来源:2018届人教版九年级数学下册同步专题练习:专项训练七 相似 题型:解答题
已知正方形ABCD的边长为1,点P为正方形内一动点,若点M在AB上,且满足△PBC∽△PAM,延长BP交AD于点N,连结CM.

(1)如图一,若点M在线段AB上,求证:AP⊥BN;AM=AN;
(2)①如图二,在点P运动过程中,满足△PBC∽△PAM的点M在AB的延长线上时,AP⊥BN和AM=AN是否成立?
②是否存在满足条件的点P,使得PC= ?(不需说明理由).
?(不需说明理由).
查看答案和解析>>
科目: 来源:2018年九年级数学(江西)北师大版下册:江西中考必考题型强化训练专题:解直角三角形应用与特殊几何图形的综合 题型:解答题
如图①所示的旅行箱的箱盖和箱底两部分的厚度相同,四边形ABCD为形如矩形的旅行箱一侧的示意图,F为AD的中点,EF∥CD.现将放置在地面上的箱子打开,使箱盖的一端点D靠在墙上,O为墙角,图②为箱子打开后的示意图.箱子厚度AD=30cm,宽度AB=50cm.
(1)图②中,EC=________cm,当点D与点O重合时,AO的长为________cm;
(2)若∠CDO=60°,求AO的长(结果取整数值,参考数据:sin60°≈0.87,cos60°=0.5,tan60°≈1.73,可使用科学计算器).

查看答案和解析>>
科目: 来源:2018年九年级数学(江西)北师大版下册:江西中考必考题型强化训练专题:解直角三角形应用与特殊几何图形的综合 题型:解答题
如图①是一副创意卡通圆规,图②是其平面示意图,OA是支撑臂,OB是旋转臂.使用时,以点A为支撑点,铅笔芯端点B可绕点A旋转作出圆.已知OA=OB=10cm.
(1)当∠AOB=18°时,求所作圆的半径(结果精确到0.01cm);
(2)保持∠AOB=18°不变,在旋转臂OB末端的铅笔芯折断了一截的情况下,作出的圆与(1)中所作圆的大小相等,求铅笔芯折断部分的长度(结果精确到0.01cm,参考数据:sin9°≈0.1564,cos9°≈0.9877,sin18°≈0.3090,cos18°≈0.9511,可使用科学计算器).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com