
科目: 来源:甘肃省2017-2018学年八年级上学期第二次月考数学试卷 题型:填空题
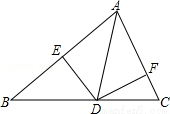
如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,DF⊥AC于点F,S△ABC=7,DE=2,AB=4,则AC长是 .
查看答案和解析>>
科目: 来源:甘肃省2017-2018学年八年级上学期第二次月考数学试卷 题型:填空题
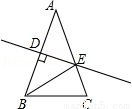
如图,在△ABC中,AB=AC=4,∠C=72°,D是AB的中点,点E在AC上,DE⊥AB,则∠ABE的度数为 .
查看答案和解析>>
科目: 来源:甘肃省2017-2018学年八年级上学期第二次月考数学试卷 题型:解答题
若10m=5,10n=3,则102m+3n= .
【答案】675.
【解析】102m+3n=102m?103n=(10m)2?(10n)3=52?33=675,
故答案为:675.
点睛:此题考查了幂的乘方与积的乘方, 同底数幂的乘法. 首先根据同底数幂的乘法法则,可得102m+3n=102m×103n,然后根据幂的乘方的运算方法,可得102m×103n=(10m)2×(10n)3,最后把10m=5,10n=2代入化简后的算式,求出102m+3n的值是多少即可.
【题型】填空题
【结束】
18
计算:
(1)(5mn2﹣4m2n)(﹣2mn)
(2)(x+7)(x﹣6)﹣(x﹣2)(x+1)
(3) (-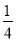 )2 016×161 008;
)2 016×161 008;
查看答案和解析>>
科目: 来源:甘肃省2017-2018学年八年级上学期第二次月考数学试卷 题型:解答题
计算:
(1)(5mn2﹣4m2n)(﹣2mn)
(2)(x+7)(x﹣6)﹣(x﹣2)(x+1)
(3) (-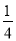 )2 016×161 008;
)2 016×161 008;
【答案】(1)﹣10m2n3+8m3n2;(2)2x﹣40;(3)1.
【解析】试题分析:(1)原式利用单项式乘以多项式法则计算即可得到结果;
(2)原式两项利用多项式乘以多项式法则计算,去括号合并即可得到结果;
(3)先根据幂的乘方的逆运算,把(-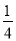 )2 016化为(
)2 016化为(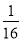 )1008,再根据积的乘方的逆运算计算即可.
)1008,再根据积的乘方的逆运算计算即可.
试题解析:(1)原式=(5mn2)(﹣2mn)+(﹣4m2n)(﹣2mn)=﹣10m2n3+8m3n2;
(2)原式=x2﹣6x+7x﹣42﹣x2﹣x+2x+2=2x﹣40.
(3)原式=(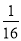 )1008×161 008=(
)1008×161 008=(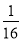 ×16)1 008=1.
×16)1 008=1.
【题型】解答题
【结束】
19
如图,方格图中每个小正方形的边长为1,点A、B、C都是格点.
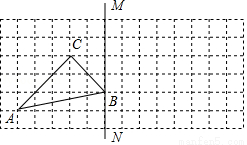
(1)画出△ABC关于直线BM对称的△A1B1C1;
(2)写出AA1的长度.
查看答案和解析>>
科目: 来源:甘肃省2017-2018学年八年级上学期第二次月考数学试卷 题型:解答题
如图,方格图中每个小正方形的边长为1,点A、B、C都是格点.
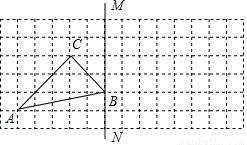
(1)画出△ABC关于直线BM对称的△A1B1C1;
(2)写出AA1的长度.
【答案】(1)详见解析;(2)AA1=10.
【解析】试题分析:(1)先作出△ABC各顶点关于直线BM对称的点,再画出△A1B1C1即可;
(2)根据图形中A,A1的位置,即可得到AA1的长度.
试题解析:(1)如图所示,△A1B1C1即为所求;
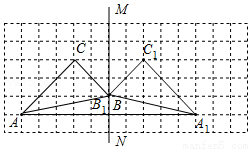
(2)由图可得,AA1=10.
【题型】解答题
【结束】
20
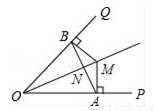
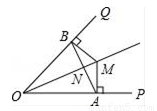
如图,OM平分∠POQ,MA⊥OP,MB⊥OQ,A、B为垂足,AB交OM于点N.求证:∠OAB=∠OBA.
查看答案和解析>>
科目: 来源:甘肃省2017-2018学年八年级上学期第二次月考数学试卷 题型:解答题
如图,OM平分∠POQ,MA⊥OP,MB⊥OQ,A、B为垂足,AB交OM于点N.求证:∠OAB=∠OBA.
【答案】证明见解析.
【解析】试题分析:先根据角平分线的性质可证得:MA=MB,
再根据HL定理判定Rt△MAO≌Rt△MBO,然后可证得:OA=OB,
根据等边对等角可证得: ∠OAB=∠OBA.
试题解析:∵OM平分∠POQ,MA⊥OP,MB⊥OQ,
∴AM=BM,
在Rt△MAO和Rt△MAO中, 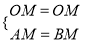 ,
,
∴Rt△AOM≌Rt△BOM(HL),
∴OA=OB,
∴∠OAB=∠OBA.
【题型】解答题
【结束】
21
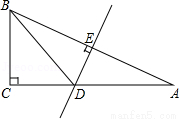
如图,在△ABC中,∠C=90°,AB的垂直平分线DE交AC于D,垂足为E,若∠A=30°,CD=3.
(1)求∠BDC的度数.
(2)求AC的长度.
查看答案和解析>>
科目: 来源:甘肃省2017-2018学年八年级上学期第二次月考数学试卷 题型:解答题
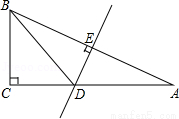
如图,在△ABC中,∠C=90°,AB的垂直平分线DE交AC于D,垂足为E,若∠A=30°,CD=3.
(1)求∠BDC的度数.
(2)求AC的长度.
【答案】(1)60°;(2)9.
【解析】试题分析:(1)由AB的垂直平分线DE交AC于D,垂足为E,根据线段垂直平分线的性质,易得AD=BD,即可求得∠ABD的度数,又由三角形外角的性质,即可求得答案;
(2)易得△BCD是含30°角的直角三角形的性质,继而求得BD的长,则可求得答案.
【解析】
(1)∵AB的垂直平分线DE交AC于D,垂足为E,
∴AD=BD,
∴∠ABD=∠A=30°,
∴∠BDC=∠ABD+∠A=60°;
(2)∵在△ABC中,∠C=90°,∠BDC=60°,
∴∠CBD=30°,
∴BD=ACD=2×3=6,
∴AD=BD=6,
∴AC=AD+CD=9.
考点:线段垂直平分线的性质;含30度角的直角三角形.
【题型】解答题
【结束】
22
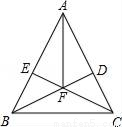
如图,在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.
求证:AF平分∠BAC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com