将图1中阴影部分的小长方形变换到图2的位置，你能根据两个图形的面积关系得到的数学公式是_____.

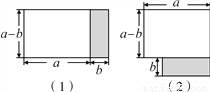
【答案】（a+b）（a-b）=a2-b2

【解析】由图可知，两个图象面积相等，（a+b）（a-b）=a2-b2.

【题型】填空题
【结束】
12

若m2-n2=6，且m-n=3，则m+n =_______________

若m2-n2=6，且m-n=3，则m+n =_______________

【答案】2

【解析】解析：∵m2-n2=（m+n）（m-n）=3（m+n）=6，

∴m+n=2.

【题型】填空题
【结束】
13

如果4x2+ax+9是一个完全平方式，那么a的值为______.

如果4x2+ax+9是一个完全平方式，那么a的值为______.

【答案】±12

【解析】解析：∵（2x±3）2=4x2±12x+9=4x2+ax+9，

∴a=±12.

【题型】填空题
【结束】
14

分解因式：ax2-ay2=______．

分解因式：ax2-ay2=______．

【答案】a（x+y）（x﹣y）

【解析】试题分析：应先提取公因式a，再对余下的多项式利用平方差公式继续分解．

【解析】
ax2﹣ay2，

=a（x2﹣y2），

=a（x+y）（x﹣y）．

故答案为：a（x+y）（x﹣y）．

点评：本题主要考查提公因式法分解因式和平方差公式分解因式，需要注意分解因式一定要彻底．

【题型】填空题
【结束】
15

已知a+b=5，ab=3，则a2+b2=______.

已知a+b=5，ab=3，则a2+b2=______.

【答案】19

【解析】试题分析：a2+b2=（a+b）2-2ab=25-6=19．

考点：完全平方公式的应用．

【题型】填空题
【结束】
16

分解因式2a（b+c）-3（b+c）的结果是______.

分解因式2a（b+c）-3（b+c）的结果是______.

【答案】（b+c）（2a-3）

【解析】解析：2a（b+c）-3（b+c）=（b+c）（2a-3）.

点睛：因式分解的方法：（1）提取公因式法.ma+mb+mc=m(a+b+c).

（2）公式法:完全平方公式，平方差公式.

（3）十字相乘法.

因式分解的时候，要注意整体换元法的灵活应用，训练将一个式子看做一个整体,利用上述方法因式分解的能力.

【题型】填空题
【结束】
17

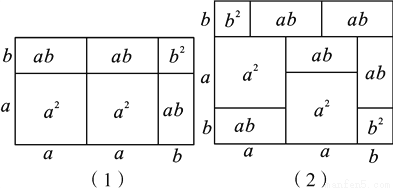
在我们所学的课本中，多项式与多项式相乘可以用几何图形的面积来表示.例如，（2a+b）（a+b）=2a2+3ab+b2就可以用图（1）来表示.请你根据此方法写出图（2）中图形的面积所表示的代数恒等式：____________.

在我们所学的课本中，多项式与多项式相乘可以用几何图形的面积来表示.例如，（2a+b）（a+b）=2a2+3ab+b2就可以用图（1）来表示.请你根据此方法写出图（2）中图形的面积所表示的代数恒等式：____________.

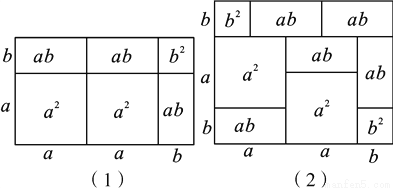
【答案】（a+2b）（2a+b）=2a2+5ab+2b2

【解析】试题分析：图②的面积可以用长为a+a+b，宽为b+a+b的长方形面积求出，也可以由四个正方形与5个小长方形的面积之和求出，表示出即可．

【解析】
根据图形列得：（a+2b）（2a+b）=2a2+5ab+2b2．

故答案为：（a+2b）（2a+b）=2a2+5ab+2b2．

考点：多项式乘多项式．

点评：此题考查了多项式乘以多项式法则，熟练掌握法则是解本题的关键．

【题型】填空题
【结束】
18

若一个正整数能表示为两个正整数的平方差，则称这个正整数为“智慧数”（如3=22-12，16=52-32，则3和16是智慧数）.已知按从小到大的顺序构成如下数列：3，5，7，8，9，11，12，13，15，16，17，19，20，21，23，24，25，…则第2 013个“智慧数”是______.

若一个正整数能表示为两个正整数的平方差，则称这个正整数为“智慧数”（如3=22-12，16=52-32，则3和16是智慧数）.已知按从小到大的顺序构成如下数列：3，5，7，8，9，11，12，13，15，16，17，19，20，21，23，24，25，…则第2 013个“智慧数”是______.

【答案】2 687

【解析】解析：观察数的变化规律，可知全部“智慧数”从小到大可按每三个数分一组，从第2组开始每组的第一个数都是4的倍数，归纳可得，第n组的第一个数为4n（n≥2）.因为2 013÷3=671，所以第2 013个“智慧数”是第671组中的第3个数，即为4×671+3=2 687.

点睛：找规律题需要记忆常见数列

1,2,3,4……n

1,3,5,7……2n-1

2,4,6,8……2n

2,4,8,16,32……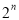

1,4,9,16,25……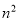

2,6,12,20……n(n+1)

一般题目中的数列是利用常见数列变形而来，其中后一项比前一项多一个常数，是等差数列，列举找规律.后一项是前一项的固定倍数，则是等比数列，列举找规律.

【题型】填空题
【结束】
19

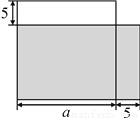
如图，郑某把一块边长为a m的正方形的土地租给李某种植，他对李某说：“我把你这块地的一边减少5 m，另一边增加5 m，继续租给你，你也没有吃亏，你看如何”.李某一听，觉得自己好像没有吃亏，就答应了.同学们，你们觉得李某有没有吃亏？请说明理由.

如图，郑某把一块边长为a m的正方形的土地租给李某种植，他对李某说：“我把你这块地的一边减少5 m，另一边增加5 m，继续租给你，你也没有吃亏，你看如何”.李某一听，觉得自己好像没有吃亏，就答应了.同学们，你们觉得李某有没有吃亏？请说明理由.

【答案】李某吃亏了，理由见解析.

【解析】试题分析：计算阴影部分面积和原正方形面积作比较.

试题解析：

【解析】
李某吃亏了.理由如下：

∵（a+5）（a-5）=a2-25＜a2，

∴李某少种了25 m2地，李某吃亏了.

【题型】解答题
【结束】
20

计算：（1）992-102×98;

（2）［x（x2y2-xy）-y（x2-x3y）］÷x2y.

计算：（1）992-102×98;

（2）［x（x2y2-xy）-y（x2-x3y）］÷x2y.

【答案】（1）-195（2）2xy-2

【解析】试题分析：（1）利用平方差公式，完全平方公式简便计算.

(2)提取公因式，化简.

试题解析：

（1）原式=（100-1）2-（100+2）×（100-2）

=（1002-200+1）-（1002-4）=-200+5=-195.

（2）原式=［x2y（xy-1）-x2y（1-xy）］÷x2y

=2x2y（xy-1）÷x2y=2（xy-1）=2xy-2.

【题型】解答题
【结束】
21

（1）先化简，再求值：a（a-2b）+（a+b）2，其中a=-1，b=;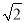

（2）若x2-5x=3，求（x-1）（2x-1）-（x+1）2+1的值.