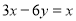相关习题
0 319397 319405 319411 319415 319421 319423 319427 319433 319435 319441 319447 319451 319453 319457 319463 319465 319471 319475 319477 319481 319483 319487 319489 319491 319492 319493 319495 319496 319497 319499 319501 319505 319507 319511 319513 319517 319523 319525 319531 319535 319537 319541 319547 319553 319555 319561 319565 319567 319573 319577 319583 319591 366461
科目:
来源:北师大版(2012) 九年级上册同步练习:1.2矩形的性质
题型:填空题
O为矩形ABCD的对角线交点,∠AOB=2∠BOC,对角线AC=12,则CB=_______.
6
【解析】∵四边形ABCD是矩形,∴∠ABC=90°,OA=OB,
∵∠AOB=2∠BOC,
∴∠AOB=120°,∠BOC=60°,∴∠CAB=30°,
∵AC=12,
∴BC=6,
故答案为:6.
查看答案和解析>>
科目:
来源:北师大版(2012) 九年级上册同步练习:1.2矩形的性质
题型:填空题
如图所示,在矩形ABCD中,AB=2BC,在CD上取点E,使AE= AB, 则∠EAB=_____,∠BEC=________.
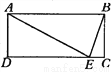
30°, 75°.
【解析】∵四边形ABCD是矩形,∴∠D=∠ABC=90°,AD=BC,DC∥AB,
∵AB=AE,AB=2CB,∴AE=2AD,∴∠DEA=30°,
∵DC∥AB,∴∠EAB=∠DEA=30°,
∵AE=AB,∴∠ABE=∠AEB=(180°-∠EAB)=75°,
∵AB//CD,∴∠BEC=∠ABE=75°,
故答案为:30°,75°.
查看答案和解析>>
科目:
来源:北师大版(2012) 九年级上册同步练习:1.2矩形的性质
题型:填空题
M为矩形ABCD的BC上一点,DN⊥AM于N,AB=3,BC=7,AM=5,则DN=______.
【解析】∵四边形ABCD是矩形,∴AD=BC=7,∠B=90°,AD//BC,
∴∠AMB=∠DAN,
∵∠AND=90°=∠B,
∴△ADN∽△MAB,
∴,即 ,∴DN= ,
故答案为: .
查看答案和解析>>
科目:
来源:北师大版(2012) 九年级上册同步练习:1.2矩形的性质
题型:解答题
如图,在矩形ABCD中,AC、BD相交于O,AE平分∠BAD,交BC于E,若∠CAE=15°,求∠BOE的度数.
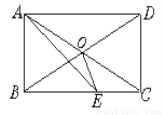
75°
【解析】试题分析:根据矩形的性质和角平分线的定义可得∠BAE=45°,再由∠CAE=15°,可求得∠BAOE=60°,可判定△AOB为等边三角形,即可得OB=AB,再证得AB=BE,即可得OB=BE,从而求得∠BOE的度数.
试题解析:
【解析】
在矩形ABCD中,∵AE平分∠BAD,
∴∠BAE=45°
又∵∠CAE=15°
∴∠BAO=∠BAE+∠...
查看答案和解析>>
科目:
来源:北师大版(2012) 九年级上册同步练习:1.2矩形的性质
题型:解答题
如图所示,矩形ABCD中,对角线AC、BD交于O点,CE⊥BD于E,OF⊥AB 于F,BE:DE=1:3,OF=2cm,求AC的长.
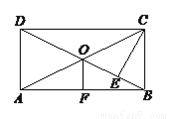
AC=8cm
【解析】试题分析:根据矩形对角线互相平分且相等,再根据BE:DE=1:3,CE⊥BD,可判断出OC=BC,再根据OF要中位线,从而可得BC的长,从而得OC的长,继而可得AC的长.
试题解析:∵四边形ABCD是矩形,
∴OA=OC=AC,OB=OD=BD,AC=BD,
∴OB=OC=OA=OD,
∵CE⊥BD,DE:BE=3:1,
∴OE=BE,
...
查看答案和解析>>
科目:
来源:北师大版(2012) 九年级上册同步练习:1.2矩形的性质
题型:解答题
如图所示,矩形ABCD中,长为7,宽为6,点E、F将BD三等分,求△AEF的面积.

7
【解析】试题分析:根据矩形的性质可得△ABD的面积是矩形面积的一半,再根据同等底等高的三角形面积相等即可得.
试题解析:∵BD是矩形ABCD的对角线,∴S△ABD=S矩形ABCD==21,
∵E、F是BD的三等分点,∴S △AEF= S△ABD=7.
查看答案和解析>>
科目:
来源:北师大版(2012) 九年级上册同步练习:1.2矩形的性质
题型:解答题
如图所示,在矩形ABCD中,四个内角平分线相交于E、F, 若AB= 8cm,Ad=20cm,求EF的长度.
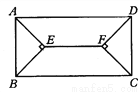
12cm
【解析】试题分析:延长BE交AD于M,延长DF交BC于N,根据矩形的性质求出∠DAE=∠BAE=∠ABE=∠CBE=45°,AD∥BC,AD=BC,求出AE⊥BM,AB=AM,得出平行四边形BMDN和平行四边形EFDM,即可求出EF=DM,求出DM即可.
试题解析:延长BE交AD于M,延长DF交BC于N,
∵四边形ABCD是矩形,
∴∠DAB=∠ABC=∠BCD=...
查看答案和解析>>
科目:
来源:北师大版(2012) 九年级上册同步练习:1.2矩形的性质
题型:解答题
如图所示,矩形ABCD沿AE折叠,使点D落在BC 边长的点F 处,如果∠BAF=60°,求∠DAE的度数.
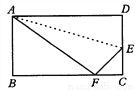
15°
【解析】试题分析:由矩形的性质可得∠BAD=90°,由∠BAF=60°,可得∠DAF=30°,再根据折叠的性质即可得.
试题解析:∵四边形ABCD是矩形,∴∠BAD=90°,
∵∠BAF=60°,∴∠DAF=∠BAD-∠BAF=30°,
∵△AFE由△ADE折叠得到,∴∠DAE=∠EAF,
∵∠DAF=∠DAE+∠EAF,
∴∠DAE=15°.
...
查看答案和解析>>
科目:
来源:北师大版(2012) 九年级上册同步练习:1.2矩形的性质
题型:解答题
某班在布置新年联欢会场,需要将直角三角形彩纸裁成长度不等的矩形彩条,如图所示,在Rt△ABC中,∠C=90°,AC=30cm,AB=50cm,依次裁下宽为1cm 的矩形纸条a1,a2,a3,…,若使裁得的矩形纸条的长都不小于5cm,问,每张直角三角形彩纸能裁成的矩形纸条总数是多少?
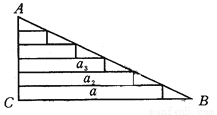
26
【解析】试题分析:把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程,通过解方程求解即可.
试题解析:Rt△ABC中,∠C=90°,AC=30cm,AB=50cm,由勾股定理可得BC=40cm,
设所求的矩形有x张,其中最小的矩形的长为ycm,
则 ,
∴y=40- ,
又∵y≥5,
∴40- ≥5,
∴x≤26,
∴最多能裁...
查看答案和解析>>
科目:
来源:重庆市华东师大版2016-2017学年七年级下学期期中考试数学试卷
题型:单选题
下列是二元一次方程的是( )
A. 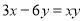 B.
B. 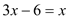 C.
C. 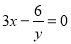 D.
D. 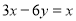
D
【解析】试题分析:A、等号右边这一项的次数是2,是二元二次方程,故A错误;
B、含一个未知数,是一元一次方程,故B错误;
C、分母中含有未知数,是分式方程,故C错误;
D、是二元一次方程,故D正确;
故选:D.
查看答案和解析>>








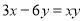 B.
B. 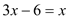 C.
C. 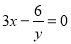 D.
D.