练习册

  • 练习册
  • 试题
    相关习题
     0  319398  319406  319412  319416  319422  319424  319428  319434  319436  319442  319448  319452  319454  319458  319464  319466  319472  319476  319478  319482  319484  319488  319490  319492  319493  319494  319496  319497  319498  319500  319502  319506  319508  319512  319514  319518  319524  319526  319532  319536  319538  319542  319548  319554  319556  319562  319566  319568  319574  319578  319584  319592  366461 

    科目： 来源：北师大版（2012） 九年级上册同步练习：1.2矩形的性质 题型：单选题

    如图所示，矩形ABCD的对角线交于O，AE⊥BD于E，∠1：∠2=2：1， 则∠1的度数为（ ）．

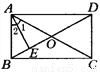
    A. 22．5° B. 45° C. 30° D. 60°

    B 【解析】∵四边形ABCD为矩形，AE⊥BD， ∴∠2+∠ABD=∠ADB+∠ABD =∠EAD+∠ADB=90°， ∴∠ADB=∠2，∠1+∠OAD+∠ADB=90°， ∵四边形ABCD是矩形，∴AO=OD，∴∠OAD=∠ADB=∠2，∴∠1+2∠2=90°， ∵∠1：∠2=2：1，∴2∠2=∠1， ∴2∠1=90°， ∴∠1=45°， 故选B....

    查看答案和解析>>

    科目： 来源：北师大版（2012） 九年级上册同步练习：1.2矩形的性质 题型：单选题

    下列叙述错误的是（ ）．

    A. 平行四边形的对角线互相平分

    B. 对角线互相平分的四边形是平行四边形

    C. 矩形的对角线相等

    D. 对角线相等的四边形是矩形

    D 【解析】A. 平行四边形的对角线互相平分，正确，不符合题意；B. 对角线互相平分的四边形是平行四边形，正确，不符合题意；C. 矩形的对角线相等，正确，不符合题意；D. 对角线相等的四边形是矩形，也可能是等腰梯形，也可能是一般四边形，故错误，符合题意， 故选D.

    查看答案和解析>>

    科目： 来源：北师大版（2012） 九年级上册同步练习：1.2矩形的性质 题型：单选题

    下列性质矩形不一定具备的是（ ）．

    A. 对角线相等 B. 四个内角都相等

    C. 对角线互相平分 D. 对角线互相垂直

    D 【解析】A.矩形的对角线相等，正确；B. 矩形的四个内角都相等，正确；C.矩形的对角线互相平分，正确；D. 对角线互相平分、相等，但不一定垂直， 故选D.

    查看答案和解析>>

    科目： 来源：北师大版（2012） 九年级上册同步练习：1.2矩形的性质 题型：填空题

    如图所示，O为矩形ABCD的对角线交点，DF平分∠ADC交AC于E，BC于F， ∠BDF=15°，则∠COF=______．

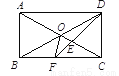
    75° 【解析】∵DF平分∠ADC，∴∠CDF=45°，∴△CDF是等腰直角三角形，∴CD=CF， ∵∠BDF=15°，∴∠CDO=∠CDF+∠BDF=45°+15°=60°， 在矩形ABCD中，OD=OC，∴△OCD是等边三角形，∴OC=CD，∠OCD=60°， ∴OC=CF，∠OCF=90°-∠OCD=90°-60°=30°， 在△COF中，∠COF= ×（180...

    查看答案和解析>>

    科目： 来源：北师大版（2012） 九年级上册同步练习：1.2矩形的性质 题型：填空题

    矩形ABCD中，AB=8，BC=6，E、F、G是AD的四等分点，则△BEF的面积是_____．

    6 【解析】连接BD，∵四边形ABCD是矩形，∴∠BAD=90°AD=BC=6，∵AB=8，∴S△ABD=×8×6=24， ∵E、F、G是AD的四等分点，∴S△BEF= S△ABD =6， 故答案为：6.

    查看答案和解析>>

    科目： 来源：北师大版（2012） 九年级上册同步练习：1.2矩形的性质 题型：填空题

    若矩形两邻边之比为3：4，周长为28cm，则它的边长为______．

    6cm, 8cm, 6cm, 8cm. 【解析】设矩形的两邻边的长分别为3xcm， 4xcm， 则有2(3x+4x) =28 ，解得x=2 ，所以3x=6，4x=8，所以矩形的边长分别为6cm， 8cm， 6cm， 8cm， 故答案为：6cm， 8cm， 6cm， 8cm.

    查看答案和解析>>

    科目： 来源：北师大版（2012） 九年级上册同步练习：1.2矩形的性质 题型：填空题

    已知矩形的对角线与较长边所夹的角等于30°，那么较短边与两对角线所围成的三角形是________三角形．

    等边 【解析】如图，矩形ABCD中，对角线AC、BD交于点O，∠OBC=30°， ∵四边形ABCD是矩形，∴∠ABC=90°，OA=OB， ∵∠OBC=30°，∴∠ABO=∠ABC-∠OBC=60°， ∴△ABO是等边三角形， 故答案为：等边.

    查看答案和解析>>

    科目： 来源：北师大版（2012） 九年级上册同步练习：1.2矩形的性质 题型：填空题

    矩形ABCD的周长为40cm，O是它的对角线交点，△AOB比△AOD周长多4cm，则它的各边长之比为________．

    8cm,12cm, 8cm ,12cm. 【解析】∵矩形ABCD的周长为40cm， ∴2（AB+AD）=40， ∴AB+AD=20， ∵△AOB比△AOD周长多4cm， ∴AO+BO+AB-AO-DO-AD=4， ∵点O是矩形ABCD的对角线的交点， ∴AO=BO=DO， ∴AB-AD=4， ∵AB+AD=20，AB-AD=4， ∴AB=...

    查看答案和解析>>

    科目： 来源：北师大版（2012） 九年级上册同步练习：1.2矩形的性质 题型：填空题

    如图所示，矩形ABCD中，AE⊥BD于E，∠DAE=3∠BAE，则∠BAE=_____，∠EAD=_____，∠EAC=_____．

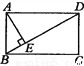
    22.5° 67.5° 45° 【解析】∵∠DAE=3∠BAE，∠DAE+∠BAE=∠BAD=90°， ∴∠BAE=22.5°，∠DAE= =67.5°， ∵AE⊥BD，∴∠AED=90°， ∴∠ADE=180-∠AED-∠EAO=22.5°， ∵矩形的对角线互相平分， ∴AO=DO， ∴∠OAD=∠ODA=22.5°， ∴∠EAO=∠BAD-∠BA...

    查看答案和解析>>

    科目： 来源：北师大版（2012） 九年级上册同步练习：1.2矩形的性质 题型：填空题

    矩形ABCD中，M为AD的中点， MB ⊥MC， 矩形的周长为24， 则AB= _____， BC=_______．

    4, 8. 【解析】∵ABCD为矩形，∴AB=DC，∠D=∠A=90°， ∵点M是AD的中点，∴AM=DM，∴△ABM≌△DCM，∴BM=CM， ∵∠BMC=90°，∴△BMC为等腰直角三角形，∴AB=AM=AD， ∵矩形ABCD的周长是24， ∴2（AB+AD）=6AB=24， ∴AB=4，BC=AD=8， 故答案为：4，8．

    查看答案和解析>>

    同步练习册答案