
科目: 来源:甘肃省定西市安定区2017-2018学年九年级上学期期末考试数学试卷 题型:解答题
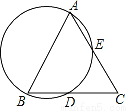
如图,点A、B、C、D、E在圆上,弦的延长线与弦的延长线相交于点,AB是圆的直径,D是BC的中点.求证:AB=AC.
查看答案和解析>>
科目: 来源:甘肃省定西市安定区2017-2018学年九年级上学期期末考试数学试卷 题型:解答题
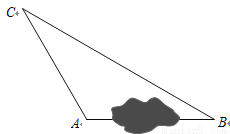
在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.现测得AC=50m,BC=100m,∠CAB=120°,请计算A,B两个凉亭之间的距离.
查看答案和解析>>
科目: 来源:甘肃省定西市安定区2017-2018学年九年级上学期期末考试数学试卷 题型:解答题
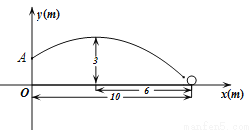
如图,在某场足球比赛中,球员甲从球门底部中心点O的正前方10m处起脚射门,足球沿抛物线飞向球门中心线;当足球飞离地面高度为3m时达到最高点,此时足球飞行的水平距离为6m.已知球门的横梁高为2.44m.
(1)在如图所示的平面直角坐标系中,问此飞行足球能否进球门?(不计其它情况)
(2)守门员乙站在距离球门2m处,他跳起时手的最大摸高为2.52m,他能阻止球员甲的此次射门吗?如果不能,他至少后退多远才能阻止球员甲的射门?
查看答案和解析>>
科目: 来源:甘肃省定西市安定区2017-2018学年九年级上学期期末考试数学试卷 题型:解答题
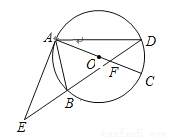
如图,⊙O的直径AC与弦BD相交于点F,点E是DB延长线上一点,∠EAB=∠ADB.
(1)求证:EA是⊙O的切线;
(2)已知点B是EF的中点,AF=4,CF=2,求AE的长.
查看答案和解析>>
科目: 来源:甘肃省定西市安定区2017-2018学年九年级上学期期末考试数学试卷 题型:解答题
如图,抛物线y=-x 2+bx+c与x轴交于A、B两点,与y轴交于点C,已知经过B、C两点的直线的表达式为y=-x+3.
(1)求抛物线的函数表达式;
(2)点P(m,0)是线段OB上的一个动点,过点P作y轴的平行线,交直线BC于D,交抛物线于E,EF∥x轴,交直线BC于F,DG∥x轴,FG∥y轴,DG与FG交于点G.设四边形DEFG的面积为S,当m为何值时S最大,最大值是多少?
(3)在坐标平面内是否存在点Q,将△OAC绕点Q逆时针旋转90°,使得旋转后的三角形恰好有两个顶点落在抛物线上.若存在,求出所有符合条件的点Q的坐标;若不存在,请说明理由.
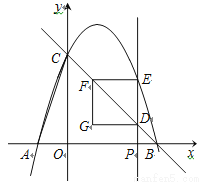
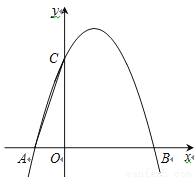
查看答案和解析>>
科目: 来源:青海省2017-2018学年七年级上学期12月月考数学试卷 题型:单选题
比-3小1的数是 ( )
A. 2 B. -2 C. 4 D. -4
D 【解析】试题解析:-3-1=-4. 故选D.查看答案和解析>>
科目: 来源:青海省2017-2018学年七年级上学期12月月考数学试卷 题型:单选题
过度包装既浪费资源又污染环境.据测算,如果全国每年减少10%的过度包装纸用量,那么可减排二氧化碳3120000吨,把数3120000用科学记数法表示为( )
A. 3.12×105 B. 3.12×106 C. 31.2×105 D. 0.312×107
B 【解析】3120000=3.12×106 故选C.查看答案和解析>>
科目: 来源:青海省2017-2018学年七年级上学期12月月考数学试卷 题型:单选题
用代数式表示“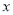 的3倍与
的3倍与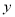 的平方的和”,正确的是( )
的平方的和”,正确的是( )
A. 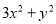 B.
B. 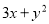 C.
C. 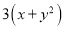 D.
D. 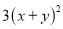
查看答案和解析>>
科目: 来源:青海省2017-2018学年七年级上学期12月月考数学试卷 题型:单选题
下列计算正确的是( )
A. 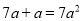 B.
B. 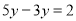 C.
C. 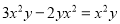 D.
D. 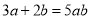
查看答案和解析>>
科目: 来源:青海省2017-2018学年七年级上学期12月月考数学试卷 题型:单选题
某物品的标价为132元,若以9折出售,仍可获利10%,则该物品的进价是( )
A.118元 B.108元 C.106元 D. 104元
B 【解析】 【解析】 设进价为x, 则依题意可列方程:132×90%x=10%•x, 解得:x=108元; 故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com