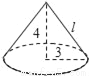
如图，圆锥的底面半径为3cm，高为4cm，那么这个圆锥的侧面积是_____cm2．

15π 【解析】试题分析：已知圆锥的底面半径为4cm，高为3cm，由勾股定理可得圆锥的母线长为5cm，根据圆锥的侧面积公式可得圆锥的侧面积为π×4×5=20πcm2．

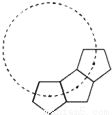
如图，若干全等正五边形排成环状．图中所示的是前3个五边形，要完成这一圆环还需_____个五边形．

7 【解析】试题分析:延长正五边形的相邻两边交于圆心，求得该圆心角的度数后，用360°除以该圆心角的度数即可得到正五边形的个数，减去3后即可得到本题答案． 【解析】 延长正五边形的相邻两边，交于圆心， ∵正五边形的外角等于360°÷5=72°， ∴延长正五边形的相邻两边围成的角的度数为：180°﹣72°﹣72°=36°， ∴360°÷36°=10， ∴排成圆环...

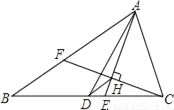
如图，在△ABC中，AB=5，AC=3，AD、AE分别为△ABC的中线和角平分线，过点C作CH⊥AE于点H，并延长交AB于点F，连结DH，则线段DH的长为_____．

1 【解析】试题分析：∵AE为△ABC的角平分线，CH⊥AE，∴△ACF是等腰三角形，∴AF=AC，∵AC=3，∴AF=AC=3，HF=CH，∵AD为△ABC的中线，∴DH是△BCF的中位线，∴DH=BF，∵AB=5，∴BF=AB﹣AF=5﹣3=2．∴DH=1，故答案为：1．

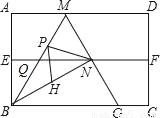
如图，四边形ABCD是矩形纸片，AB=2．对折矩形纸片ABCD，使AD与BC重合，折痕为EF；展平后再过点B折叠矩形纸片，使点A落在EF上的点N，折痕BM与EF相交于点Q；再次展平，连接BN，MN，延长MN交BC于点G．有如下结论：

①∠ABN=60°；②AM=1；③QN=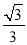；④△BMG是等边三角形；⑤P为线段BM上一动点，H是BN的中点，则PN+PH的最小值是．

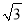其中正确结论的序号是_____．

①④⑤ 【解析】如图1,连接AN, ∵EF垂直平分AB， ∴AN=BN， 根据折叠的性质，可得 AB=BN， ∴AN=AB=BN. ∴△ABN为等边三角形。 ∴∠ABN=60°,∠PBN=60°÷2=30°， 即结论①正确； ∵∠ABN=60°，∠ABM=∠NBM， ∴∠ABM=∠NBM=60°÷2=30°， ∴AM=AB?t...

计算：（）﹣2﹣（π﹣）0+|﹣2|+4sin60°．

5+ 【解析】原式=4﹣1+2﹣+4×=5+．

解不等式组

-2≤x<. 【解析】试题分析：先分别求出两个不等式的解集，再找出它们的公共部分. 试题解析： 【解析】 解不等式4（x+1）≤7x+10，得：x≥－2， 解不等式x－5＜，得：x＜， 则不等式组的解集为：－2≤x＜.

先化简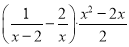，再从0，1，2中选一个合适的x的值代入求值．

. 【解析】试题分析：原式括号中两项通分并利用同分母分式的减法法则计算，约分得到最简结果，把x=1代入计算即可求出值． 试题解析：原式= ? =， 当x=1时,原式=.

为解决“最后一公里”的交通接驳问题，某市投放了大量公租自行车使用，到2014年底，全市已有公租自行车25000辆，租赁点600个，预计到2016年底，全市将有公租自行车50000辆，并且平均每个租赁点的公租自行车数量是2014年底平均每个租赁点的公租自行车数量的1.2倍，预计到2016年底，全市将有租赁点多少个？

1000个. 【解析】试题分析：根据租赁点的公租自行车数量变化表示出2014年和2016年平均每个租赁点的公租自行车数量，进而得出等式求出即可． 试题解析：设到2016年底,全市将有租赁点x个, 根据题意可得： =， 解得：x=1000， 经检验得：x=1000是原方程的根， 答：到2016年底，全市将有租赁点1000个。

关于的一元二次方程x2+2x+k+1=0的有两个实数解是x1和x2．

（1）求k的取值范围；

（2）如果x1+x2－x1x2＜－1且k为整数，求k的值．

（1）k≤0；（2）k的值为－1和0． 【解析】试题分析：（1）∵方程有实数根 ∴⊿=22-4k+1）≥0解得 k≤0. （2）根据一元二次方程根与系数的关系，得x1+x2=-2, x1x2=k+1 得 -2—（ k+1）＜-1 解得 k＞-2 ∴ -2＜k≤0 ∵k为整数 ∴k的值为-1和0. 试题解析：【解析】 ∵（1）方程有实数根 ∴⊿=22-4k+1）≥0....

A、B、C三人玩篮球传球游戏，游戏规则是：第一次传球由A将球随机地传给B、C两人中的某一人，以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人．

（1）求两次传球后，球恰在B手中的概率；

（2）求三次传球后，球恰在A手中的概率．

（1）；（2） . 【解析】试题分析：（1）直接列举出两次传球的所有结果，球球恰在B手中的结果只有一种即可求概率；（2）画出树状图，表示出三次传球的所有结果，三次传球后，球恰在A手中的结果有2种，即可求出三次传球后，球恰在A手中的概率． 试题解析: 【解析】 （1）两次传球的所有结果有4种，分别是A→B→C，A→B→A，A→C→B，A→C→A．每种结果发生的可能性相等，球球恰在...