
科目: 来源:黄金30题系列 八年级数学 小题好拿分 题型:填空题
已知关于x的方程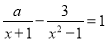 有增根,则a的值等于__.
有增根,则a的值等于__.
查看答案和解析>>
科目: 来源:黄金30题系列 八年级数学 小题好拿分 题型:填空题
如果从一卷粗细均匀的电线上截取1米长的电线,称得它的质量为a克,再称得剩余电线的质量为b克,那么原来这卷电线的总长度是__________米.
+1 【解析】试题分析:这卷电线的总长度=截取的1米+剩余电线的长度. 试题解析:根据1米长的电线,称得它的质量为a克,只需根据剩余电线的质量除以a,即可知道剩余电线的长度.故总长度是(+1)米.查看答案和解析>>
科目: 来源:黄金30题系列 八年级数学 小题好拿分 题型:填空题
等腰三角形的两边长分别是4cm和6cm,则它的周长是_________.
16或14 【解析】试题分析:根据等腰三角形的性质,分两种情况:①当腰长为6cm时,②当腰长为4cm时,解答出即可; 试题解析:根据题意, ①当腰长为6cm时,周长=6+6+4=16(cm); ②当腰长为4cm时,周长=4+4+6=14(cm).查看答案和解析>>
科目: 来源:黄金30题系列 八年级数学 小题好拿分 题型:填空题
△ABC中,∠A=30°,当∠B=________ 时,△ABC是等腰三角形.
75°或30°或120° 【解析】试题分析:当∠A为顶角等于30°时,可得底角∠B=(180°-30°)=75°,△ABC是等腰三角形,当∠A=∠B=30°时,△ABC是等腰三角形,当∠A=∠C=30°时,则∠B=120°,△ABC是等腰三角形,故答案为:75°或30°或120°.查看答案和解析>>
科目: 来源:黄金30题系列 八年级数学 小题好拿分 题型:填空题
如图,△ABC的角平分线 CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②CA平分∠BCG;③∠ADC=∠GCD;④∠DFB=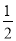 ∠CGE.
∠CGE.
其中正确的结论是_____________(填序号).
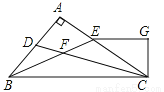
查看答案和解析>>
科目: 来源:黄金30题系列 八年级数学 小题好拿分 题型:填空题
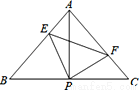
已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出的以下四个结论:①AE=CF; ②△EPF一定是等腰直角三角形; ③S四边形AEPF=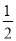 S△ABC;④当∠EPF在△ABC内绕顶点P旋转时始终有EF=AP。(点E不与A、B重合),上述结论中始终正确的有_____.(写序号)
S△ABC;④当∠EPF在△ABC内绕顶点P旋转时始终有EF=AP。(点E不与A、B重合),上述结论中始终正确的有_____.(写序号)
查看答案和解析>>
科目: 来源:2017年安徽省合肥市高新区梦园学校中考数学模拟试卷 题型:单选题
计算1-(-2)的正确结果是( )
A. -2 B. -1 C. 1 D. 3
D 【解析】分析:本题利用有理数的减法计算即可. 解析:原式 故选D.查看答案和解析>>
科目: 来源:2017年安徽省合肥市高新区梦园学校中考数学模拟试卷 题型:单选题
(am)m•(am)2不等于( )
A. (am+2)m B. (am•a2)m C. 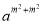 D. (am)3•(am﹣1)m
D. (am)3•(am﹣1)m
查看答案和解析>>
科目: 来源:2017年安徽省合肥市高新区梦园学校中考数学模拟试卷 题型:单选题
下列各组中运算结果相等的是( )
A. 23与32 B. (﹣2)4与﹣24 C. (﹣2)3与﹣23 D. (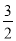 )2与(
)2与(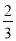 )2
)2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com