某药品经过两次降价，每瓶零售价由168元降为128元，已知两次降价的百分率相同，每次降价的百分率为x，根据题意列方程得________．

168（1﹣x）2=128 【解析】试题分析：因为每次降价的百分率为x，所以降一次后每瓶零售价为168（1-x），降两次后每瓶零售价为，所以．

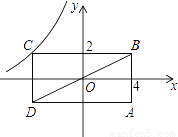
如图，矩形ABCD的对角线BD经过坐标原点，矩形的边分别平行于坐标轴，点C在反比例函数y= 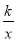的图象上，若点A的坐标为（4，﹣2），则k的值为________．

-8 【解析】由题意得：点 在 上，则

请写出一个无实数根的一元二次方程_________

x2﹣x+3=0 【解析】试题分析：写出一个元二次方程，然后确定根的判别式的值小于0即可． 如：对于方程x2-x+3=0，因为△=12-4×1×3=-12＜0，所以x2-x+3=0无实数根．

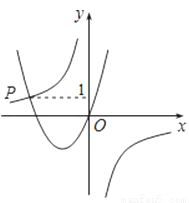
如图，已知函数y=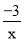与y=ax2+bx+c（a＞0，b＞0）的图象相交于点P，且点P的纵坐标为1，则关于x的方程ax2+bx+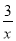=0的解是________ 

x=﹣3，y=1 【解析】试题解析：∵P的纵坐标为1， ∴1=-， ∴x=-3， ∵ax2+bx+=0化为于x的方程ax2+bx=-的形式， ∴此方程的解即为两函数图象交点的横坐标的值， ∴x=-3．

从1，2，3这三个数字中任意抽取两个，其和是偶数的概率是________．

【解析】首先根据题意画出树状图，然后由树状图求得所有等可能的结果与其和是偶数的情况，再利用概率公式即可求得答案． 【解析】 画树状图得： ∵共有6种等可能的结果，其和是偶数的2种情况， ∴其和是偶数的概率是：=． 故答案为：．

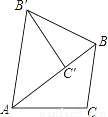
如图，把△ABC绕点A逆时针旋转42°，得到△AB′C′，点C′恰好落在边AB上，连接BB′，则∠B′BC′的大小为________．

69° 【解析】【解析】 ∵把△ABC绕点A逆时针旋转42°，得到△AB′C′，点C′恰好落在边AB上，∴∠BAB′=42°，AB=AB′，∴∠AB′B=∠ABB′，∴∠B′BC′= （180°﹣42°）=69°．故答案为：69°．

在一个不透明的布袋中有除颜色外其它都相同的红、黄、蓝球共200个，某位同学经过多次摸球试验后发现，其中摸到红色球和蓝色球的频率稳定在35%和55%，则口袋中可能有黄球________个．

20 【解析】根据频率估计概率得到摸到红色球和蓝色球的概率分别为35%和55%，则摸到黄色球的概率=1-35%-55%=10%，所以口袋中黄球的个数=200×10%=20．

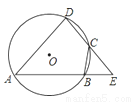
如图，已知A、B、C、D是⊙O上的四点，延长DC、AB相交于点E．若BC=BE．求证：△ADE是等腰三角形．

证明见解析. 【解析】试题分析：求出 即可得出，从而判定等腰三角形． 试题解析： 四点共圆， 即是等腰三角形．

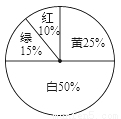
某商场为了吸引顾客，设立了一个可以自由转动的转盘（如下图），并规定：购买100元的商品，就能获得一次转动转盘的机会，如果转盘停止后，指针正好对准红、绿、黄、白区域，那么顾客就可以分别得到80元、30元、10元、0元的购物券，凭购物券仍然可以在商场购物；如果顾客不愿意转转盘，那么可以直接获得购物券10元．

（1）每转动一次转盘所获购物券金额的平均数是多少？

（2）若在此商场购买100元的货物，那么你将选择哪种方式获得购物券？

（3）小明在家里也做了一个同样的转盘做实验，转10次后共获得购物券96元，他说还是不转转盘直接领取购物券合算，你同意小明的说法吗？请说明理由．

（1）15元；（2）选择转动转盘，理由见解析；（3）小明的说法不正确. 【解析】试题分析：（1）根据相应金额和百分比可得到每转动一次转盘所获购物券金额的平均数； （2）由（1）结果和10比较得到结果； （3）概率是大量实验得到的结论． 试题解析：【解析】 （1）15%×30+10%×80+25%×10=15元； （2）选择转动转盘，因为由（1）得转动转盘的平均获取金...

已知关于x的一元二次方程x2+3x+1﹣m=0有两个不相等的实数根．

（1）求m的取值范围；

（2）若m为负整数，求此时方程的根．

（1）m的取值范围为m＞﹣ ；（2）当m=﹣1时，此方程的根为x1=﹣1和x2=﹣2． 【解析】试题分析：（1）由方程有两个不等实数根可得b2﹣4ac＞0，代入数据即可得出关于m的一元一次不等式，解不等式即可得出结论； （2）根据m为负整数以及（1）的结论可得出m的值，将其代入原方程，利用分解因式法解方程即可得出结论． 试题解析：（1）∵关于x的一元二次方程x2+3x+1﹣m=0...