
科目: 来源:福建省南平市2018届九年级上学期第二次月考数学试卷 题型:填空题
从实数―1,―2,1中随机选取两个数,积为负数的概率是__________.
【解析】从实数-1、-2、1中随机选取两个数共有以下三种等可能情况:①-1,-2;②-1,1;③-2,1;其中乘积为负数的是②、③两种, ∴从实数-1,-2,1中随机选取两个数,积为负数的概率是: . 故答案为: .查看答案和解析>>
科目: 来源:福建省南平市2018届九年级上学期第二次月考数学试卷 题型:填空题
如图,在△ABC中,∠BAC=50°,AC=2,AB=3,将△ABC绕点A逆时针旋转50°,得到△AB1C1,则阴影部分的面积为_______.
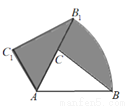
查看答案和解析>>
科目: 来源:福建省南平市2018届九年级上学期第二次月考数学试卷 题型:填空题
已知关于x的方程x2﹣6x+k=0的两根分别 是x1,x2,且满足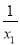 +
+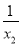 =3,则k的值是 _______.
=3,则k的值是 _______.
查看答案和解析>>
科目: 来源:福建省南平市2018届九年级上学期第二次月考数学试卷 题型:填空题
如图,在⊙O的内接五边形ABCDE中,∠CAD=30°,则∠B+∠E= .
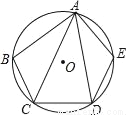
查看答案和解析>>
科目: 来源:福建省南平市2018届九年级上学期第二次月考数学试卷 题型:填空题
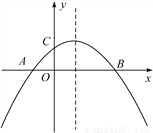
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:①abc<0;②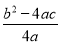 >0;③ac-b+1=0;④OA·OB=-
>0;③ac-b+1=0;④OA·OB=-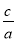 .其中结论正确的是____________
.其中结论正确的是____________
查看答案和解析>>
科目: 来源:福建省南平市2018届九年级上学期第二次月考数学试卷 题型:解答题
解方程 (1)x2+6x+1=0 (2)(x﹣1)2=2(1﹣x)
(1)x=-3+ 2,x=-3-2;(2)x=1,x=-1. 【解析】试题分析: (1)根据方程特点,用“公式法”或“配方法”解答本题即可; (2)根据方程特点,用“因式分解法”解答本题即可. 试题解析: (1)∵在方程中, , ∴△=, ∴, ∴. (2)原方程移项得: , ∴, ∴或, 解得: .查看答案和解析>>
科目: 来源:福建省南平市2018届九年级上学期第二次月考数学试卷 题型:解答题
一个不透明的布袋里装有3个球,其中2个红球,1个白球,它们除颜色外其余都相同.
(1)求摸出1个球是白球的概率;
(2)摸出1个球,记下颜色后放回,并搅均,再摸出1个球.求两次摸出的球恰好颜色不同的概率(要求画树状图或列表);
(3)现再将n个白球放入布袋,搅均后,使摸出1个球是白球的概率为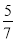 .求n的值.
.求n的值.
查看答案和解析>>
科目: 来源:福建省南平市2018届九年级上学期第二次月考数学试卷 题型:解答题
如图为桥洞的形状,其正视图是由弧CD和矩形ABCD构成.O点为弧CD所在⊙O的圆心,且点O恰好在水面AB上.若桥洞跨度CD为8米,拱高(OE⊥弦CD于点F )EF为2米.求弧CD所在⊙O的半径DO.
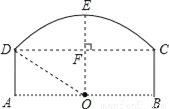
查看答案和解析>>
科目: 来源:福建省南平市2018届九年级上学期第二次月考数学试卷 题型:解答题
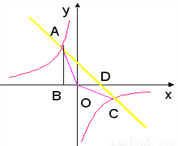
点A是双曲线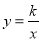 与直线
与直线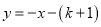 在第二象限的交点,AB垂直
在第二象限的交点,AB垂直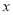 轴于点B,且S△ABO=
轴于点B,且S△ABO=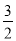 .
.
(1)求两个函数的表达式;
(2)求直线与双曲线的交点坐标和△AOC的面积.
查看答案和解析>>
科目: 来源:福建省南平市2018届九年级上学期第二次月考数学试卷 题型:解答题
我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销.每天销售量(y件)与销售单价x(元/件)的函数关系式是y=﹣10x+700
(1)当销售单价定为多少时,试销该工艺品每天获得的利润最大?最大利润是多少?
(2)市物价部门规定,该工艺品销售单价最高不能超过35元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?
(1)销售单价定为40元/件时,利润最大,最大利润为每天9000元;(2)当销售单价定为35元/件时,每天所获利润最大,最大利润为每天8750元. 【解析】试题分析: (1)设每天获得的利润为w,根据总利润=单件商品利润×商品销售量可得,w=(x-10)(-10x+700),整理、配方即可求得当x为多少时,w有最大值及最大值是多少; (2)估计(1)中所得配方后的w与x间的函数关...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com