练习册

  • 练习册
  • 试题
    相关习题
     0  320473  320481  320487  320491  320497  320499  320503  320509  320511  320517  320523  320527  320529  320533  320539  320541  320547  320551  320553  320557  320559  320563  320565  320567  320568  320569  320571  320572  320573  320575  320577  320581  320583  320587  320589  320593  320599  320601  320607  320611  320613  320617  320623  320629  320631  320637  320641  320643  320649  320653  320659  320667  366461 

    科目： 来源：数学人教版八年级上册第11章第二节与三角形有关的角第三课时同步练习 题型：填空题

    AB∥CD，BC与AD相交于点M，N是射线CD上一点．若∠B＝65°，∠MDN＝135°，则∠AMB＝_______．

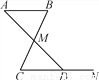
    70° 【解析】试题分析：∵AB∥CD， ∴∠A+∠MDN=180°， ∴∠A=180°﹣∠MDN=45°， 在△ABM中，∠AMB=180°﹣∠A﹣∠B=70°． 故答案为：70°．

    查看答案和解析>>

    科目： 来源：数学人教版八年级上册第11章第二节与三角形有关的角第三课时同步练习 题型：解答题

    已知：如图，∠2是△ABC的一个外角．

    求证：∠2=∠A+∠B．

    证明：如图，

    ∵∠A+∠B+∠1=180° （ ）

    ∠1+∠2=180° （ ）

    ∴∠2=∠A+∠B （ ）

    三角形内角和定理；邻补角的定义；等量代换 【解析】试题分析：根据三角形内角和定理和平角的定义得出∠A+∠B+∠1=180°，∠1+∠2=180°，从而得出∠A+∠B+∠1=∠1+∠2，即∠2=∠A+∠B． 试题解析：证明：∵∠A+∠B+∠1=180°(三角形内角和定理)， ∠1+∠2=180°(邻补角的定义)， ∴∠2=∠A+∠B(等量代换)． 故答案为：三角形内角和...

    查看答案和解析>>

    科目： 来源：数学人教版八年级上册第11章第二节与三角形有关的角第三课时同步练习 题型：填空题

    如图所示，直线a∥b，∠1=130°，∠2=70°，求则∠3的度数．

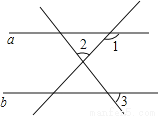
    70° 【解析】试题分析：先根据三角形的外角的性质求得∠4的度数，再根据平行线的性质求解即可. ∵∠1＝130°，∠2＝70° ∴∠4＝130°-70°＝60° ∵a//b ∴∠3＝∠4＝60°.

    查看答案和解析>>

    科目： 来源：数学人教版八年级上册第11章第二节与三角形有关的角第三课时同步练习 题型：解答题

    已知：如图，在△ABC中，∠B=∠C，AD平分外角∠EAC．

    求证：AD∥BC．

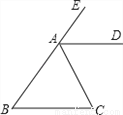
    证明见解析 【解析】试题分析：由角平分线的定义可知：∠EAD=∠EAC，再由三角形的外角的性质可得∠EAD=∠B，然后利用平行线的判定定理可证明出结论. 试题解析：∵AD平分∠EAC， ∴∠EAD=∠EAC． 又∵∠B=∠C，∠EAC=∠B+∠C， ∴∠B=∠EAC． ∴∠EAD=∠B． 所以AD∥BC．

    查看答案和解析>>

    科目： 来源：数学人教版八年级上册第11章第二节与三角形有关的角第三课时同步练习 题型：解答题

    如图，在△ABC中，∠B=47°，三角形的外角∠DAC和∠ACF的平分线交于点E，求∠AEC的度数．

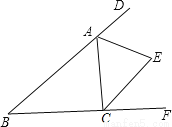
    66.5° 【解析】试题分析：根据三角形内角和定理、角平分线的定义以及三角形外角定理求得∠DAC+∠ACF=（∠B+∠B+∠1+∠2）=；最后在△AEC中利用三角形内角和定理可以求得∠AEC的度数． 试题解析： ∵三角形的外角∠DAC和∠ACF的平分线交于点E， ∴∠EAC=∠DAC，∠ECA=∠ACF； 又∵∠B=47°（已知），∠B+∠1+∠2=180°（三角形内...

    查看答案和解析>>

    科目： 来源：数学人教版八年级上册第11章第二节与三角形有关的角第三课时同步练习 题型：解答题

    如图，∠ACD是△ABC的外角，∠ABC的平分线与∠ACD的平分线交于点A1，∠A1BC的平分线与∠A1CD的平分线交于点A2，…，∠An﹣1BC的平分线与∠An﹣1CD的平分线交于点An．设∠A=θ．则：

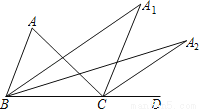
    （1）求∠A1的度数；

    （2）∠An的度数．

    （1）∠A1=；（2）∠An= 【解析】（1）∵BA1是∠ABC的平分线，CA1是∠ACD的平分线， ∴∠A1BC=∠ABC，∠A1CD=∠ACD， 又∵∠ACD=∠A+∠ABC，∠A1CD=∠A1BC+∠A1， ∴（∠A+∠ABC）=∠ABC+∠A1， ∴∠A1=∠A， ∵∠A=θ， ∴∠A1=； （2）同理可得∠A2=∠A1=•=， 所以∠...

    查看答案和解析>>

    科目： 来源：湖北省武汉市江夏区2018届九年级上期末模拟数学试卷 题型：填空题

    在分别写有﹣1，0，1，2的四张卡片中随机抽取一张，所抽取的数字平方后等于1的概率为 ________.

    【解析】试题解析：因为-1，0，1，2的四张卡片中随机抽取一张，所抽取的数字平方后等于1共有2张， 所以所抽取的数字平方后等于1的概率为，

    查看答案和解析>>

    科目： 来源：湖北省武汉市江夏区2018届九年级上期末模拟数学试卷 题型：填空题

    把方程2x2﹣1=x（x+3）化成一般形式是________．

    x2﹣3x﹣1=0 【解析】2x2﹣1=x（x+3）， 2x2﹣1=x2+3x， 则2x2﹣x2﹣3x﹣1=0， 故x2﹣3x﹣1=0， 故答案为：x2﹣3x﹣1=0．

    查看答案和解析>>

    科目： 来源：湖北省武汉市江夏区2018届九年级上期末模拟数学试卷 题型：填空题

    抛物线y=ax2+bx+c上部分点的横坐标x，纵坐标y的对应值如下表：

    x

    …

    ﹣2

    ﹣1

    0

    1

    2

    …

    y

    …

    0

    4

    6

    6

    4

    …

    则抛物线的对称轴是________．

    x= 【解析】试题分析：观察表格可得抛物线过（0,6），（1,6），所以可得抛物线的对称轴是x=．

    查看答案和解析>>

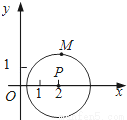
    科目： 来源：湖北省武汉市江夏区2018届九年级上期末模拟数学试卷 题型：填空题

    如图，以点P（2，0）为圆心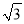， 为半径作圆，点M（a，b）是⊙P上的一点，则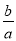的最大值是________ ．

    【解析】试题分析：当有最大值时，得出tan∠MOP有最大值，推出当OM与圆相切时，tan∠MOP有最大值，根据解直角三角形得出tan∠MOP=，由勾股定理求出OM，代入求出即可． 试题解析：当有最大值时，得出tan∠MOP有最大值， 也就是当OM与圆相切时，tan∠MOP有最大值， 此时tan∠MOP=， 在Rt△OMP中，由勾股定理得：OM=1， 则tan∠MOP=...

    查看答案和解析>>

    同步练习册答案