
科目: 来源:浙江省宁波市东钱湖九校2018届九年级上册期中联考数学试卷 题型:填空题
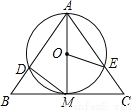
如图,已知AM为⊙O的直径,直线BC经过点M,且AB=AC,∠BAM=∠CAM,线段AB和AC分别交⊙O于点D、E,∠BMD=40°,则∠EOM=________.
查看答案和解析>>
科目: 来源:浙江省宁波市东钱湖九校2018届九年级上册期中联考数学试卷 题型:填空题
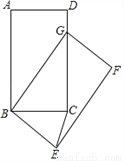
如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF,点A落在矩形ABCD的边CD上,连接CE,则CE的长是__________.
查看答案和解析>>
科目: 来源:浙江省宁波市东钱湖九校2018届九年级上册期中联考数学试卷 题型:解答题
甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
(1)(2)不公平 【解析】试题分析:(1)利用列表法得到所有可能出现的结果,根据概率公式计算即可; (2)分别求出甲、乙获胜的概率,比较即可. 试题解析:(1)所有可能出现的结果如图: 从表格可以看出,总共有9种结果,每种结果出现的可能性相同,其中两人抽取相同数字的结果有3种,所以两人抽取相同数字的概率为: ; (2)不公平, 从表格可以看出,两人抽取数字和为...查看答案和解析>>
科目: 来源:浙江省宁波市东钱湖九校2018届九年级上册期中联考数学试卷 题型:解答题
如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.
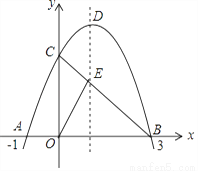
(1)求此抛物线的解析式;
(2)直接写出点C和点D的坐标;
(3)若点P在第一象限内的抛物线上,且S△ABP=4S△COE , 求P点坐标.
(1)y=-x2+2x+3(2)D(1,4)(3)P(2,3) 【解析】试题分析:(1)将A、B的坐标代入抛物线的解析式中,即可求出待定系数b、c的值,进而可得到抛物线的对称轴方程; (2)令x=0,可得C点坐标,将函数解析式配方即得抛物线的顶点C的坐标; (3)设P(x,y)(x>0,y>0),根据题意列出方程即可求得y,即得D点坐标. (1)由点A(﹣1,0)和点B(3...查看答案和解析>>
科目: 来源:浙江省宁波市东钱湖九校2018届九年级上册期中联考数学试卷 题型:解答题
如图,AB是⊙O的直径,BC是⊙O的弦,半径OD⊥BC,垂足为E,若BC=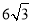 ,DE=3.
,DE=3.
求:
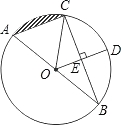
(1)⊙O的半径;
(2)弦AC的长;
(3)阴影部分的面积.
(1)6;(2)6;(3)6π-9. 【解析】 试题分析:(1)半径OD⊥BC,所以由垂径定理知:CE=BE,在直角△OCE中,根据勾股定理就可以求出OC的值; (2)根据AB是⊙O的直径,得到∠ACB=90°,因而在直角三角形ABC中根据勾股定理得到AC的长; (3)阴影部分的面积就是扇形OCA的面积减去△OAC的面积. 试题解析:(1)∵半径OD⊥BC, ∴...查看答案和解析>>
科目: 来源:浙江省宁波市东钱湖九校2018届九年级上册期中联考数学试卷 题型:解答题
如图某幢大楼顶部有广告牌CD.张老师目高MA为1.60米,他站立在离大楼45米的A处测得大楼顶端点D的仰角为30°;接着他向大楼前进14米、站在点B处,测得广告牌顶端点C的仰角为45°.(取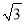 ≈1.732 ,计算结果保留一位小数)
≈1.732 ,计算结果保留一位小数)
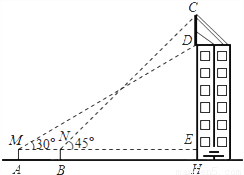
(1)求这幢大楼的高DH;
(2)求这块广告牌CD的高度.
(1)27.6米(2)广告牌CD的高度为5.0米 【解析】试题分析:首先分析图形:根据题意构造直角三角形Rt△DME与Rt△CNE;应利用ME﹣NE=AB=14构造方程关系式,进而可解即可求出答案. 试题解析:【解析】 (1)在Rt△DME中,ME=AH=45米; 由tan30°= ,得DE=45×=15×1.732=25.98米; 又因为EH=MA=1.6米,因而大楼D...查看答案和解析>>
科目: 来源:浙江省宁波市东钱湖九校2018届九年级上册期中联考数学试卷 题型:解答题
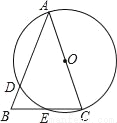
如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.
(1)求证:BE=CE;
(2)若BD=2,BE=3,求AC的长.
查看答案和解析>>
科目: 来源:浙江省宁波市东钱湖九校2018届九年级上册期中联考数学试卷 题型:解答题
甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x﹣4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.
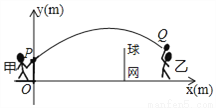
(1)当a=﹣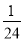 时,①求h的值;②通过计算判断此球能否过网.
时,①求h的值;②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为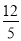 m的Q处时,乙扣球成功,求a的值.
m的Q处时,乙扣球成功,求a的值.
查看答案和解析>>
科目: 来源:浙江省宁波市东钱湖九校2018届九年级上册期中联考数学试卷 题型:解答题
(2016浙江省宁波市)从三角形(不是等腰三角形)一个顶点引出一条射线于对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线.
(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数.
(3)如图2,△ABC中,AC=2,BC=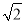 ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
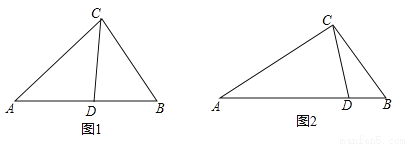
查看答案和解析>>
科目: 来源:山东省临朐县沂山风景区2018届九年级上期末模拟数学试卷 题型:单选题
如果两个相似三角形对应边的比为2:3,那么这两个相似三角形面积的比是( )
A. 2:3 B. 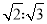 C. 4:9 D. 8:27
C. 4:9 D. 8:27
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com