
科目: 来源:2017年安徽省中考数学三模试卷 题型:解答题
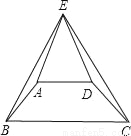
已知如图,等腰梯形ABCD,AB=CD,BE=CE,求证:AE=DE.
查看答案和解析>>
科目: 来源:2017年安徽省中考数学三模试卷 题型:解答题
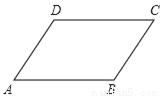
如图,已知平行四边形ABCD.
(1)用直尺和圆规作出么ABC的平分线BE,交AD的延长线于点E,交DC于点F(保留作图痕迹,不写作法);
(2)求证:△ABE是等腰三角形;
(3)在(1)中所得图形中,除△ABE外,请你写出其他的等腰三角形.(不要求证明)
查看答案和解析>>
科目: 来源:2017年安徽省中考数学三模试卷 题型:解答题
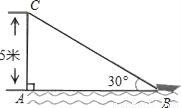
如图,在离水面高度为5m的岸上有人用绳子拉船靠岸,开始绳子与水面的夹角为30°,此人以每秒0.5m的速度收绳.
(1)8秒后船向岸边移动了多少米?
(2)写出还没收的绳子的长度S米与收绳时间t秒的函数关系式.
查看答案和解析>>
科目: 来源:2017年安徽省中考数学三模试卷 题型:解答题
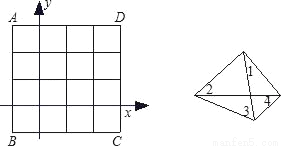
如图,放在平面直角坐标系中的正方形ABCD的边长为4,现做如下实验:抛掷一枚均匀的正四面体骰子(如图,它有四个顶点,各顶点数分别是1、2、3、4),每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的点数作为直角坐标系中点P的坐标(第一次的点数为横坐标,第二次的点数为纵坐标).
(1)求点P落在正方形面上(含边界,下同)的概率;
(2)将正方形ABCD平移数个单位,是否存在一种平移,使点P落在正方形面上的概率为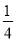 ?若存在,指出其中的一种平移方式;若不存在,说明理由.
?若存在,指出其中的一种平移方式;若不存在,说明理由.
查看答案和解析>>
科目: 来源:2017年安徽省中考数学三模试卷 题型:解答题
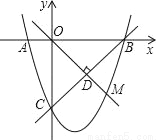
如图所示,已知抛物线y=ax2+bx+c过点A(﹣1,0),且经过直线y=x﹣3与坐标轴的两个交点B、C.
(1)求抛物线的表达式;
(2)若点M在第四象限内且在抛物线上,有OM⊥BC,垂足为D,求点M的坐标.
查看答案和解析>>
科目: 来源:2017年安徽省中考数学三模试卷 题型:解答题
市政公司为绿化建设路风景带,计划购买甲乙两种树苗600株,甲种树苗每株50元,乙种树苗每株70元.有关统计表明,甲乙两种树苗的成活率分别为80%和95%.(注:成活率= ×100%).
×100%).
(1)若购买树苗的钱不超过40000元,应如何选购甲、乙两种树苗;
(2)若希望这批树苗的成活率不低于90%,且购买树苗的费用最低,应如何选购甲、乙两种树苗并求出最低费用是多少元.
(1)选购甲种树苗不少于100株,乙种树苗不超过500株;(2)购买甲种树苗200株,乙种树苗400株时费用最低,最低费用是38000元. 【解析】【试题分析】 (1)根据总费用,列出不等式即可.设选购甲种树苗x株,则选购乙种树苗为(600﹣x)株,根据题意得,50x+70(600﹣x)≤40000,解得x≥100,即选购甲种树苗不少于100株,乙种树苗不超过500株. (2)设...查看答案和解析>>
科目: 来源:安徽省宿州市(城西校区) 2017-2018学年九年级第一学期期中测试数学试卷 题型:单选题
从﹣ ,0,
,0,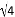 ,π,3.5这五个数中,随机抽取一个,则抽到无理数的概率是( )
,π,3.5这五个数中,随机抽取一个,则抽到无理数的概率是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目: 来源:安徽省宿州市(城西校区) 2017-2018学年九年级第一学期期中测试数学试卷 题型:单选题
袋子里有4个球,标有2,3,4,5,先抽取一个并记住,放回,然后再抽取一个,所抽取的两个球数字之和大于6的概率是( )
A.  B.
B. 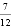 C.
C.  D.
D. 
查看答案和解析>>
科目: 来源:安徽省宿州市(城西校区) 2017-2018学年九年级第一学期期中测试数学试卷 题型:单选题
如图,已知菱形ABCD的边长为3,∠ABC=60°,则对角线AC的长是( )
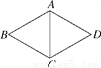
A. 12 B. 9 C. 6 D. 3
D 【解析】 ∵四边形ABCD是菱形, ∴AB=BC, ∴△ABC是等腰三角形, ∵∠ABC=60°, ∴△ABC是等边三角形, ∴AB=BC=AC, ∵菱形ABCD的边长为3, ∴AB=BC=3, ∴AC=3. 故本题应选D.查看答案和解析>>
科目: 来源:安徽省宿州市(城西校区) 2017-2018学年九年级第一学期期中测试数学试卷 题型:单选题
如图,已知四边形ABCD是平行四边形,下列结论中错误的是( )
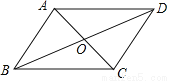
A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
D 【解析】试题分析:A、根据邻边相等的平行四边形是菱形可知四边形ABCD是菱形,故本选项不符合题意; B、根据对角线垂直的平行四边形是菱形可知四边形ABCD是菱形,故本选项不符合题意; C、根据有一个角是直角的平行四边形是矩形可知四边形ABCD是矩形,故本选项不符合题意; D、根据对角线相等的平行四边形是矩形可知四边形ABCD是矩形,但不一定是正方形,故本选项符合题意. ...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com