
科目: 来源:辽宁省2018届九年级上学期期末考试数学试卷 题型:填空题
正六边形的边长为1,则它的面积是__________
【解析】【解析】 ∵此多边形为正六边形,∴∠AOB=360°÷6=60°,∵OA=OB,∴△OAB是等边三角形,∴OA=AB=1cm,∴OG=OA•cos30°=1×=,∴S△OAB=×AB×OG=×1×=cm,∴S六边形=6S△OAB=6×=cm.故答案为: .查看答案和解析>>
科目: 来源:辽宁省2018届九年级上学期期末考试数学试卷 题型:填空题
如图,在矩形ABCD中,已知AB=8,BC=6,矩形在直线上绕其右下角的顶点B向右旋转90°
至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置……以此类推,这样连续旋转2018
次后,顶点A在整个旋转过程中所经过的路线之和是_________

查看答案和解析>>
科目: 来源:辽宁省2018届九年级上学期期末考试数学试卷 题型:解答题
如图,点O、B的坐标分别为(0,0)、(3,0),将△OAB绕O点按逆时针方向旋转90°得到△0A′B′。在图中画出△0A′B′并求出点A′的坐标
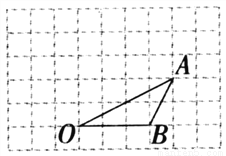
查看答案和解析>>
科目: 来源:辽宁省2018届九年级上学期期末考试数学试卷 题型:解答题
已知关于x的一元二次方程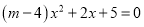 有实数根
有实数根
(1)求m的取值范围
(2)当m取最大整数值时,求出该方程的根
(1),(2) . 【解析】试题分析:(1)由关于x的一元二次方程有实数根,则m﹣4≠0且△≥0,解不等式得到m的取值范围; (2)由m的取值范围,可确定m的最大整数值,将m的最大整数值代入原方程,即可求出该方程两根. 试题解析:【解析】 (1) 由题意得:m﹣4≠0且△≥0,∵,解得 ,∴m的取值范围是且; (2)由(1)得m=3,此时方程为,即. 配方得,∴ ,...查看答案和解析>>
科目: 来源:辽宁省2018届九年级上学期期末考试数学试卷 题型:解答题
某校9年2班有2名男生和3名女生报名参加志愿者活动。若从报名者中随机选取2名学生参加志愿者活动,请你用列表法或画树状图求选取的两名学生是一男一女的概率
【解析】试题分析:列举出所有情况,看选取的两名学生是一男一女的情况数占总情况数的多少即可. 试题解析:【解析】 画树状图如图: 由树状图可得出:共有20种情况,由树状图可知共有20种等可能结果,其中选取的2名学生是一男一女的结果有12种,所以概率为 .查看答案和解析>>
科目: 来源:辽宁省2018届九年级上学期期末考试数学试卷 题型:解答题
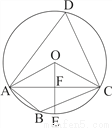
如图,四边形ABCD 是⊙O的内接四边形,∠ABC=2∠D,连接OA,OC,AC
(1)求∠OCA的度数 (2)如果OE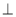 AC于F,且OC=
AC于F,且OC=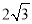 , 求AC的长
, 求AC的长
查看答案和解析>>
科目: 来源:辽宁省2018届九年级上学期期末考试数学试卷 题型:解答题
随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了个圆形喷水池,在水池中心竖直安装了一根高为2米的喷水管,它喷出的抛物线形水柱在与水池中心的水平距离为1米处达到最高,水柱落地处离池中心3米.
(1)请你建立适当的平面直角坐标系,并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度的多少?

查看答案和解析>>
科目: 来源:辽宁省2018届九年级上学期期末考试数学试卷 题型:解答题
列方程解应用题:
某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按480元销售时,每天可销售160个;若销售单价每降低1元,每天可多售出2个,已知每个玩具的固定成本为360元,问这种玩具的销售单价为多少元时,厂家每天可获利润20000元?
这种玩具的销售单价为460元时,厂家每天可获利润20000元. 【解析】试题分析:设这种玩具的销售单价为x元时,厂家每天可获利润元,根据销售单价每降低元,每天可多售出个可得现在销售[160+2(480-x)]个,再利用获利润元,列一元二次方程解求解即可. 试题解析: 【解】 【解析】 设这种玩具的销售单价为x元时,厂家每天可获利润元,由题意得, (x-360)[16...查看答案和解析>>
科目: 来源:辽宁省2018届九年级上学期期末考试数学试卷 题型:解答题
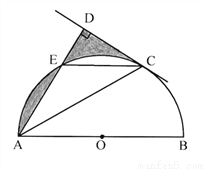
如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD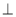 CD,垂足为D,AD交⊙O 于E,连接CE.(1)求证:CD 是⊙O 的切线
CD,垂足为D,AD交⊙O 于E,连接CE.(1)求证:CD 是⊙O 的切线
(2)若E是弧AC的中点,⊙O 的半径为1,求图中阴影部分的面积。
查看答案和解析>>
科目: 来源:辽宁省2018届九年级上学期期末考试数学试卷 题型:解答题
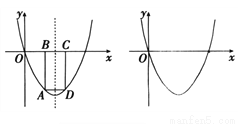
已知:抛物线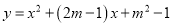 经过坐标原点,且当
经过坐标原点,且当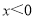 时, y随x的增大而减小.
时, y随x的增大而减小.
(1)求抛物线的解析式;
(2)如下图,设点A是该抛物线上位于x轴下方的一个动点,过点A作x轴的平行线交抛物线于另一点D,再作AB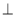 x轴于点B, DC
x轴于点B, DC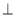 x轴于点C.
x轴于点C.
①当 BC=1时,直接写出矩形ABCD的周长;
②设动点A的坐标为(a, b),将矩形ABCD的周长L表示为a的函数,并写出自变量的取值范围,判断周长是否存在最大值,如果存在,求出这个最大值,并求出此时点A的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com